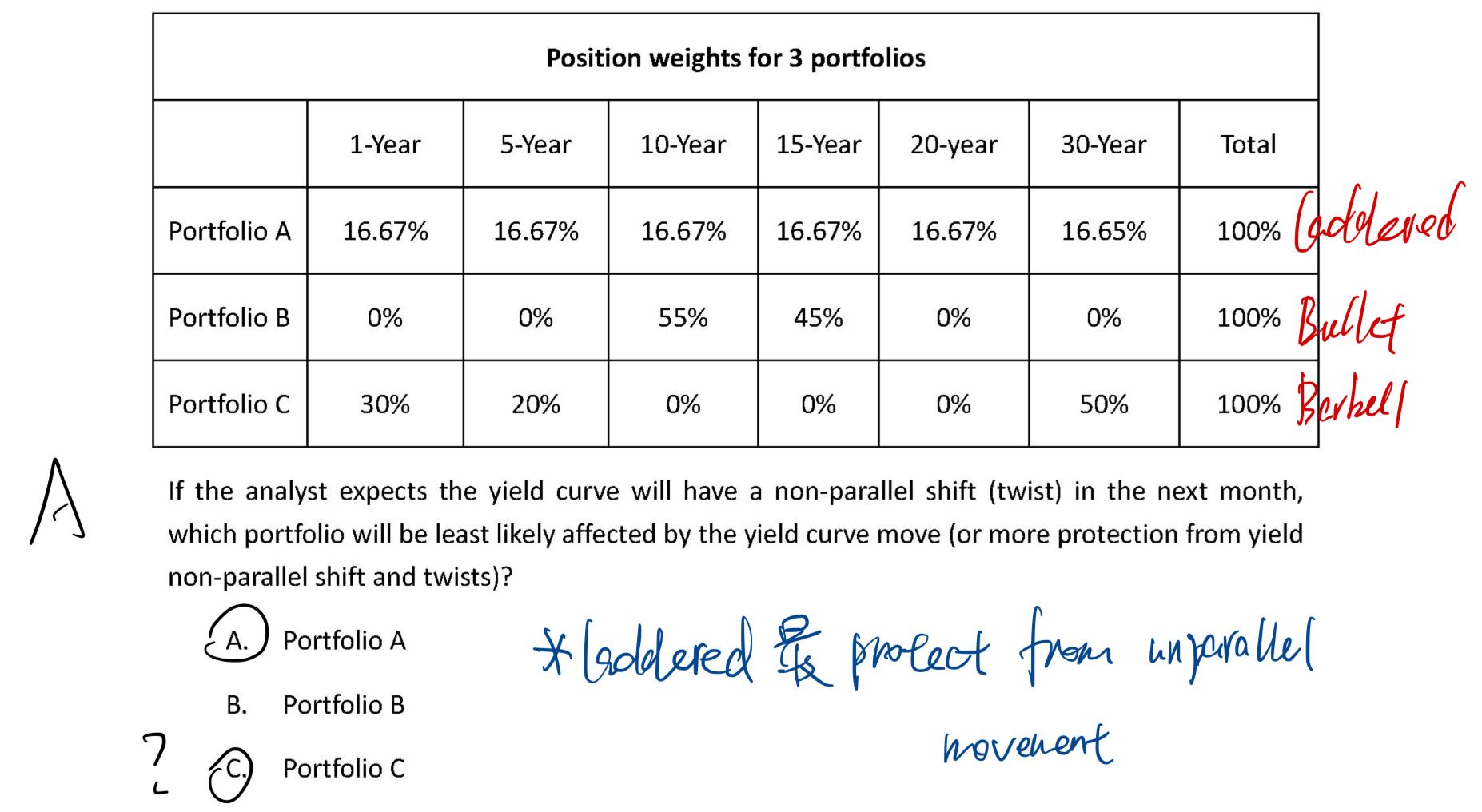
y一般不是bullet的convexity最小,所以sturctural risk最小吗?为什么这道题选laddered?考试的时候遇到类似的题,我应该怎么做?还是看convexity吗?
发亮_品职助教 · 2024年08月12日
structural risk最小的不是convexity最小的吗?y一般不是bullet的convexity最小,所以sturctural risk最小吗?为什么这道题选laddered?考试的时候遇到类似的题,我应该怎么做?还是看convexity吗?
在duration一致的情况下,确实是convexity越小,构建duration-matching的structural risk就越小。
bullet, barbell, laddered,三者在duration相同时,bullet的convexity最小。所以如果是构建duration-matching的话,bullet的structural risk最小。
但这个题和duration-matching没有关系了,他考的不是structural risk的话题。这个是考查laddered portfolio的一个自身属性:在利率曲线非平行移动时,laddered的表现基本很稳定,而barbell和bullet的表现很极端。
Laddered portfolio的这种稳定就表述为:非平行移动时,laddered portfolio能提供更多的protection。
原因是这样:
在非平行移动时,Barbell与bullet要么不会受到影响,要么影响就很大,他们表现就是非常极端、不稳定。
例如,2-year和20-year的barbell。假设非平行移动是10-year的利率发生改变。这时候barbell的组合就基本没有影响。因为影响组合的利率只是2-year和20-year的利率。这时候在这种非平行移动下,barbell的表现就非常稳定。
如果非平行移动是2-year和20-year的利率发生上升,这时候barbell就会受到极大的影响。因为发生改变的利率就恰好是现金流大权重的利率,组合的value波动极大。这时候的非平行移动,对barbell的影响很大。
所以同样是非平行移动,barbell的表现就很极端。当非平行移动时,改变的利率是现金流大权重的利率,组合的影响就会很大。当改变的利率不是现金流大权重的利率,组合基本不受影响。
bullet的分析同理。本质原因就是,barbell与bullet的现金流过于集中在特定的利率点上。
而laddered的特征就是现金流非常分散,每个期限上都有一点现金流,且权重都不大。所以不管是哪种形式的非平行移动,组合都会受到影响,但影响不大。
所以,不管是咋样的非平行移动,Laddered组合的表现都很稳定。于是说非平行移动下,laddered会有更多的protection。
其实本质原因就是:laddered的现金流是比较均匀地分散在各个期限上。如下是原版书的描述,其实就是上面的解释:
barbell与bullet在非平行移动时,有very different outcomes。但laddered的显著优势是protection from shifts and twists,原因是他的现金流是diversified across time specturm,现金流均匀地分布在各个期限上。
A non-parallel shift or a twist in the curve, however, leads to very different outcomes for the bullet and barbell structures. An obvious advantage to the laddered portfolio is protection from shifts and twists—the cash flows are essentially “diversified” across the time spectrum
这道题没有duration-matching的背景哈,duration-matching的话要在满足条件的基础上,尽可能追求资产convexity小,本质是要求资产和负债的数据尽可能接近,即资产很像负债,在这种情况下,structural risk不匹配的风险就会比较小。
发亮_品职助教 · 2024年08月13日
duration-matching下的理解没有问题,convexity越小,structural risk就越小。但是如果不做duration-matching,就不涉及structural risk,因为structural risk是duraiton-matching不成功的风险,不做Duration-mathing就不考虑这点哈。