NO.PZ2022123002000064
问题如下:
Hood believes that bond yields will begin an upward trend and wants
to adjust the duration of the balanced fund’s fixed income portfolio for the
next two years. Bullseye’s head trader informs Hood that he can implement this
duration adjustment using a pay-fixed, receive-floating interest rate swap.
Hood considers the
selected swap contracts shown in Exhibit 2. He knows that he can obtain the
required interest rate exposure using any one of these contracts, but his
objective is to minimize the notional principal of the swap.
Exhibit 2 Selected Pay-Fixed, Receive-Floating Swap Contracts

Determine
which counterparty’s swap contract will best achieve Hood’s objective. Justify
your response.
选项:
解释:
Correct Answer:
The Canis swap contract will best achieve Hood’s objective because it
is the alternative with the smallest required notional principal. The duration
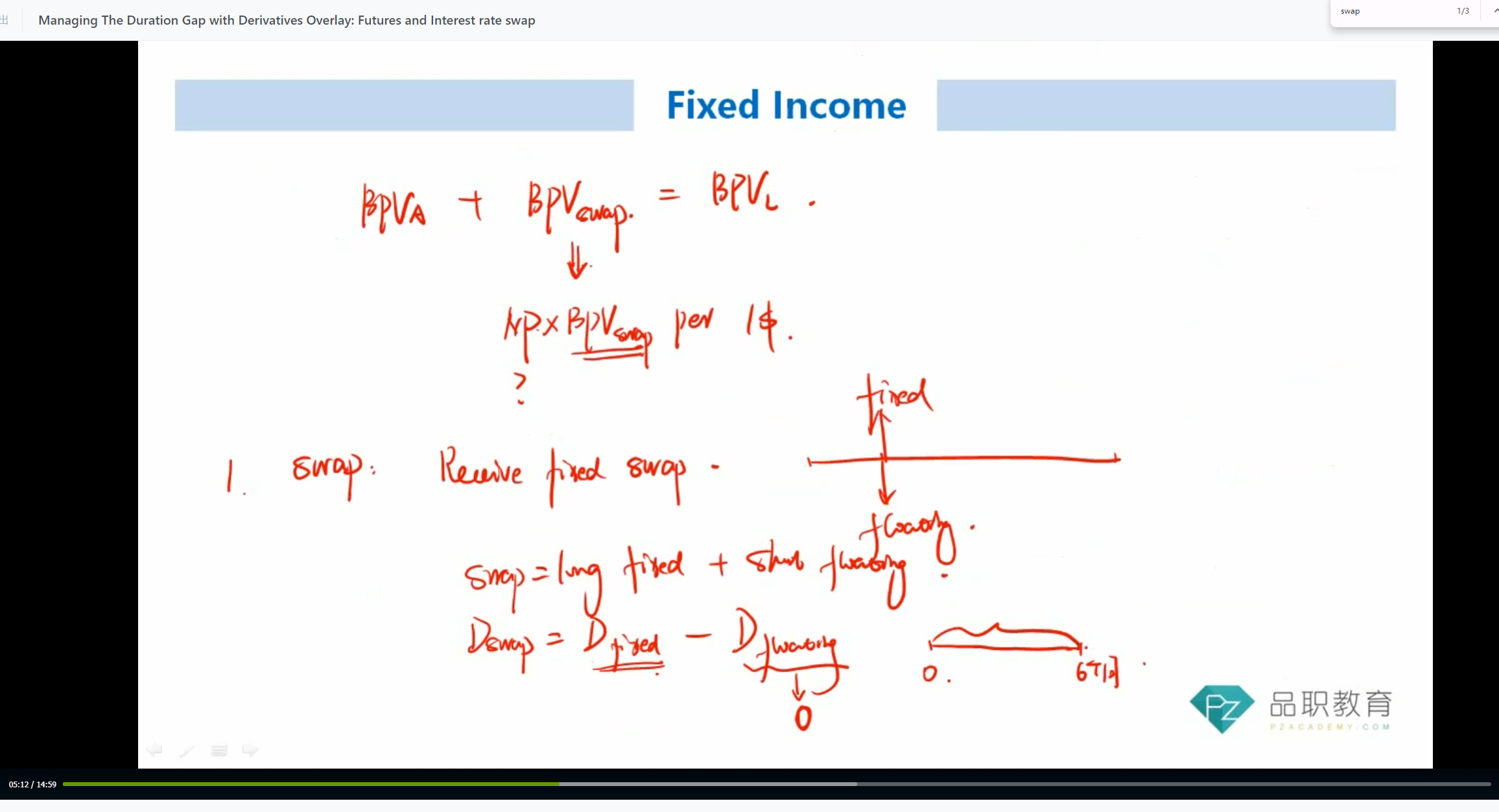
of a pay-fixed, receive-floating interest rate swap is equal to the duration of
a floating-rate bond minus the duration of a fixed-rate bond, where the bonds
have cash flows equivalent to the corresponding cash flows of the swap. The
duration of the fixed leg is 75% of its maturity and the duration of the
floating leg is 50% of its payment frequency period.
The swap duration for each swap in Exhibit 2 is calculated below:
Swap duration =
Duration of floating leg – Duration of fixed leg
Duration of Orion contract (three-year maturity with quarterly
payments) = 0.125 – 2.25 = –2.125
Duration
of Ursa contract (three-year maturity with semiannual payments) = 0.25 – 2.25 =
–2.00
Duration
of Canis contract (five-year maturity with quarterly payments) = 0.125 – 3.75 =
–3.625
Duration
of Lupus contract (five-year maturity with semiannual payments) = 0.25 – 3.75 =
–3.50
In this case, because the Canis contract has the longest maturity and
the highest payment frequency, its duration is the most negative of the four
alternatives.
The notional principal of a swap (with duration MDURS) needed to change
the duration of a bond portfolio, with a market value of B, from its current
duration of MDURB to a target duration of MDURT is calculated as: NP = B x
[(MDURT – MDURB)/MDURS)
Therefore using a swap with a higher (negative) duration requires a
lower notional principal (NP) for the same-sized adjustment to portfolio
duration.
老师,答案的知识点好像有点印象,但具体查找讲义又没找到,可否麻烦老师讲解一下?谢谢!