NO.PZ2020011303000086
问题如下:
Suppose that the current volatility estimate is 3% per day and the long-run average volatility estimate is 2% per day. What are the volatility estimates in ten days and 100 days in a GARCH (1,1) model where ω= 0.000002, α= 0.04, and β= 0.94?
解释:
The expected variance rate in ten days is 0.02^2 + (0.04 + 0.94)^10 (0.03^2– 0.02^2) = 0.000809,
题目问:现在是volatility=3%,long-run average volatility=2%,利用GARCH(1,1)来计算10天和100天的volatility,ω= 0.000002, α= 0.04, and β= 0.94。
10天volatility=[0.02^2 + (0.04 + 0.94)^10 (0.03^2– 0.02^2)]^0.5 = 2.84%.
100天volatility=[0.02^2 + (0.04 + 0.94)^100 (0.03^2 – 0.02^2)]^0.5 = 2.16%.
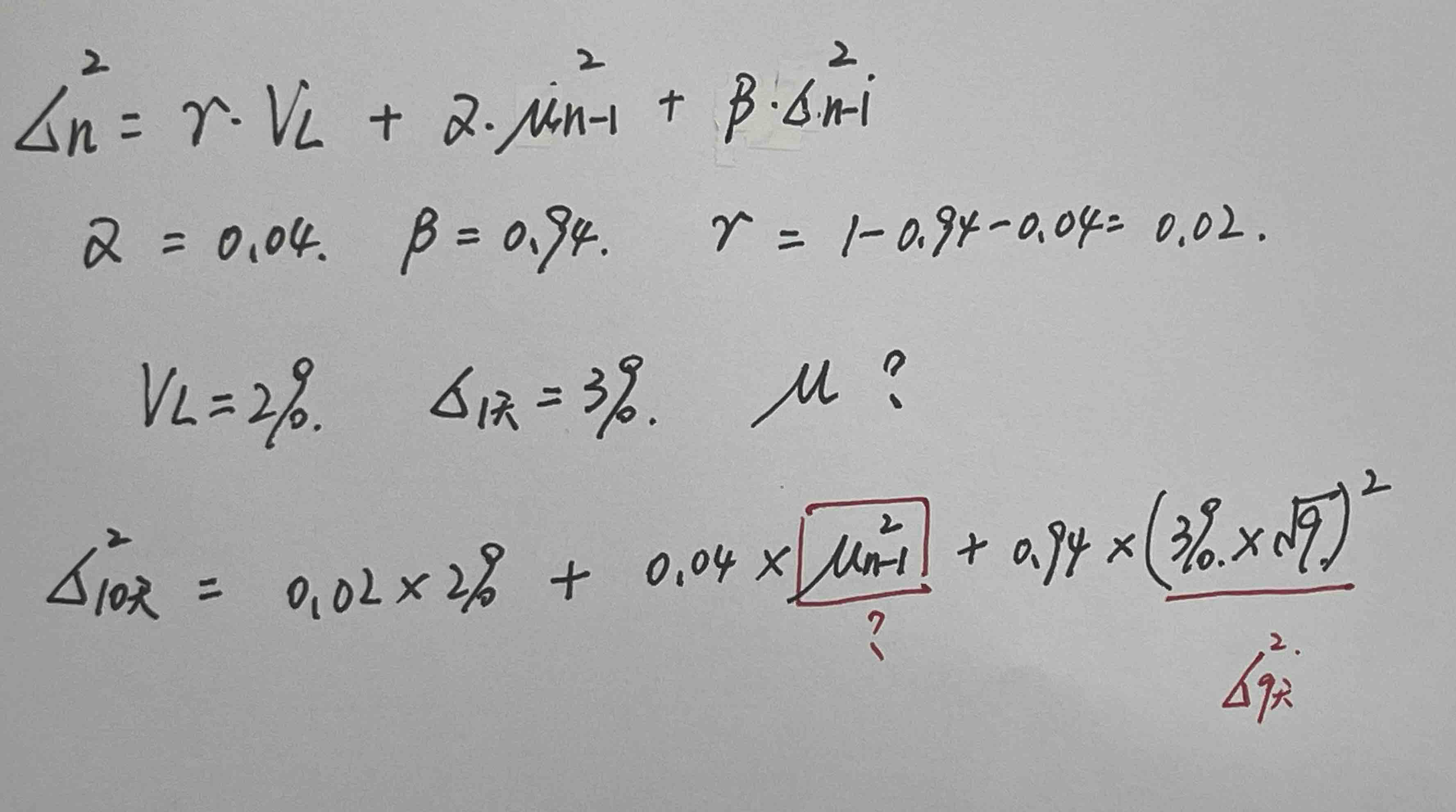
老师好,看不懂答案,1、这道题哪里的表述能看出u啊?也就是收益率?2、还有我写出的表达式除了不知道u(n-1),有其他哪里不对的地方吗?



