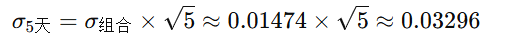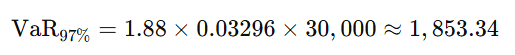开发者:上海品职教育科技有限公司 隐私政策详情

应用版本:4.2.11(IOS)｜3.2.5(安卓)APP下载

返回

梦梦 · 2024年07月24日

资产组合的VaR

  1. FRM I
  2. Valuation And Risk Models

NO.PZ2020011303000068

问题如下：

Consider a position consisting of a USD 10,000 investment in asset X and a USD 20,000 investment in asset Y. Assume that the daily volatilities of X and Y are 1% and 2% and that the coefficient of correlation between their returns is 0.3. What is the five-day VaR with a 97% confidence level?

解释：

The standard deviation of the daily changes in the assets are (in USD) 100 and 400. The standard deviation of the daily change in the portfolio is (100^2+400^2+2×100×400×0.3)^0.5=440.5

The standard deviation of the five-day change is the square root of 5 multiplied by the one-day standard deviation, which is USD 984.9. The 97% VaR is 1.88 times this, which is USD 1852.4.

题目问：有一个头寸包含10,000$的资产X，20,000$的资产Y，假设每日波动是1%和2%，相关系数是0.3，求5天97%的VaR?

每日波动的dollar值：X=10,000*1%=100，Y=20,000*2%=400

组合每日的波动=(100^2+400^2+2×100×400×0.3)^0.5=440.5

5天97%的VAR=440.5*(5)^0.5*1.88=1852.4

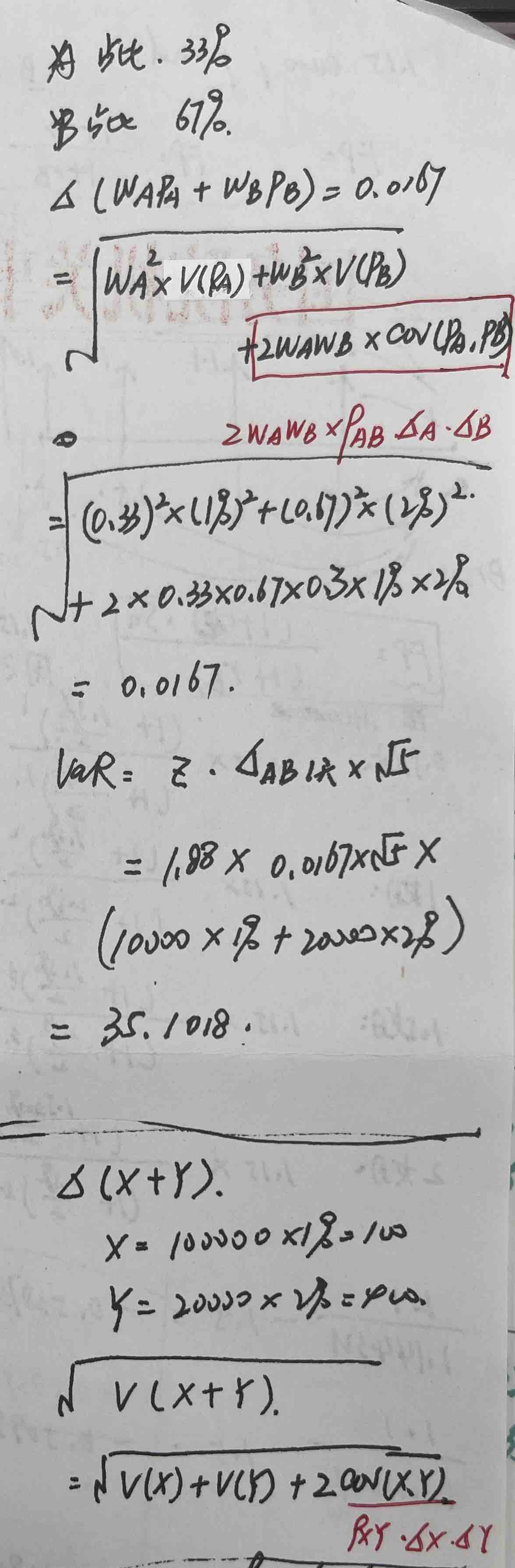
老师好，1、黑线上半部分我哪里想的不对吗？2、答案的解析，也就是黑线下半部分，我不明白为什么V（X+Y）就直接用100和400来算了，我明白100和400是怎么来的哈，但是100和400只是资产价值啊，100^2难道就相当于V（X）？400^2相当于V（Y）？cov（X，Y）相当于0.3*100*400？不懂答案的含义是什么意思，100就是西格玛X？400就是西格玛Y？3、如果用excel计算的话，有概率计算分位点是什么函数？有分位点计算累计概率又是什么函数呢

添加评论
2 个答案
已采纳答案

pzqa39 · 2024年07月25日

嗨，努力学习的PZer你好：


1、你的组合方差算出来是0.0167，但其实应该是0.00021712，正确的标准差是0.01474，列的数据并没有错，应该是按错了吧？这就导致后面都错了，不能计算出正确的结果。

 

最后计算五天的波动率应该是：

计算VaR应该是：

可能因为保留小数位数不同，存在误差，但是可以看到结果基本相近。

2、100和400并不是资产价值，而是每日波动值（标准差）。这些值通过以下公式计算得出：

资产X的每日波动值：10,000美元 × 1% = 100美元

资产Y的每日波动值：20,000美元 × 2% = 400美元

这意味着在计算组合的方差时，我们使用的是这些资产的每日波动值（标准差）。

后面你说的都是正确的。

3、函数：NORM.INV

用法：NORM.INV(probability, mean, standard_dev)

这个函数用于计算给定概率下的分位点。例如，如果你想知道在正态分布中97%的分位点，你可以使用这个函数。

函数：NORM.DIST

用法：NORM.DIST(x, mean, standard_dev, cumulative)

解释：这个函数用于计算给定分位点下的累计概率。cumulative参数为TRUE表示计算累计分布函数（CDF），为FALSE表示计算概率密度函数（PDF）。

----------------------------------------------
就算太阳没有迎着我们而来，我们正在朝着它而去，加油！

梦梦 · 2024年07月27日

明白了，1、但是计算器算了好几遍(100^2+400^2+2×100×400×0.3)^0.5=440.5，不得440.5，等于426.6145…2、在用excel公式的时候，NORM.INV后面要录三个值？比如“= NORM.INV（95%，0，1）？假设是标准正态分布哈

pzqa39 · 2024年07月28日

嗨，爱思考的PZer你好：


1、再算一下，答案是没有错的呢。根号下（10000+160000+24000），是440.45

2、是的

----------------------------------------------
加油吧，让我们一起遇见更好的自己！

梦梦 · 2024年08月01日

好的，我再算一下，谢谢

  • 2

    回答

  • 0

    关注

  • 82

    浏览
相关问题

NO.PZ2020011303000068问题如下Consir a position consisting of a US10,000 investment in asset X ana US20,000 investment in asset Y. Assume ththe ily volatilities of X anY are 1% an2% anththe coefficient of correlation between their returns is 0.3. Whis the five-y Vwith a 97% confinlevel? The stanrviation of the ily changes in the assets are (in US 100 an400. The stanrviation of the ily change in the portfolio is (100^2+400^2+2×100×400×0.3)^0.5=440.5The stanrviation of the five-y change is the square root of 5 multipliethe one-y stanrviation, whiis US984.9. The 97% Vis 1.88 times this, whiis US1852.4. 题目问有一个头寸包含10,000$的资产X，20,000$的资产Y，假设每日波动是1%和2%，相关系数是0.3，求5天97%的VaR?每日波动的llar值X=10,000*1%=100，Y=20,000*2%=400组合每日的波动=(100^2+400^2+2×100×400×0.3)^0.5=440.55天97%的VAR=440.5*(5)^0.5*1.88=1852.4 老师您好，这是您之前对某个学生的解答，但有两个问题，第一个您帮我看看我的公式有问题吗，我算了很多遍都是2.16%，并不是1.47%。第二个问题是方法二为什么不计算X资产和Y资产的权重呢？

2024-03-03 18:57 2 · 回答

NO.PZ2020011303000068问题如下 Consir a position consisting of a US10,000 investment in asset X ana US20,000 investment in asset Y. Assume ththe ily volatilities of X anY are 1% an2% anththe coefficient of correlation between their returns is 0.3. Whis the five-y Vwith a 97% confinlevel? The stanrviation of the ily changes in the assets are (in US 100 an400. The stanrviation of the ily change in the portfolio is (100^2+400^2+2×100×400×0.3)^0.5=440.5The stanrviation of the five-y change is the square root of 5 multipliethe one-y stanrviation, whiis US984.9. The 97% Vis 1.88 times this, whiis US1852.4. 题目问有一个头寸包含10,000$的资产X，20,000$的资产Y，假设每日波动是1%和2%，相关系数是0.3，求5天97%的VaR?每日波动的llar值X=10,000*1%=100，Y=20,000*2%=400组合每日的波动=(100^2+400^2+2×100×400×0.3)^0.5=440.55天97%的VAR=440.5*(5)^0.5*1.88=1852.4 97%1.88是怎么来的求画图。。。

2023-05-08 20:49 1 · 回答

NO.PZ2020011303000068问题如下Consir a position consisting of a US10,000 investment in asset X ana US20,000 investment in asset Y. Assume ththe ily volatilities of X anY are 1% an2% anththe coefficient of correlation between their returns is 0.3. Whis the five-y Vwith a 97% confinlevel? The stanrviation of the ily changes in the assets are (in US 100 an400. The stanrviation of the ily change in the portfolio is (100^2+400^2+2×100×400×0.3)^0.5=440.5The stanrviation of the five-y change is the square root of 5 multipliethe one-y stanrviation, whiis US984.9. The 97% Vis 1.88 times this, whiis US1852.4. 题目问有一个头寸包含10,000$的资产X，20,000$的资产Y，假设每日波动是1%和2%，相关系数是0.3，求5天97%的VaR?每日波动的llar值X=10,000*1%=100，Y=20,000*2%=400组合每日的波动=(100^2+400^2+2×100×400×0.3)^0.5=440.55天97%的VAR=440.5*(5)^0.5*1.88=1852.4 最后算var的时候乘以金额

2023-03-17 17:24 1 · 回答

NO.PZ2020011303000068问题如下Consir a position consisting of a US10,000 investment in asset X ana US20,000 investment in asset Y. Assume ththe ily volatilities of X anY are 1% an2% anththe coefficient of correlation between their returns is 0.3. Whis the five-y Vwith a 97% confinlevel? The stanrviation of the ily changes in the assets are (in US 100 an400. The stanrviation of the ily change in the portfolio is (100^2+400^2+2×100×400×0.3)^0.5=440.5The stanrviation of the five-y change is the square root of 5 multipliethe one-y stanrviation, whiis US984.9. The 97% Vis 1.88 times this, whiis US1852.4. 题目问有一个头寸包含10,000$的资产X，20,000$的资产Y，假设每日波动是1%和2%，相关系数是0.3，求5天97%的VaR?每日波动的llar值X=10,000*1%=100，Y=20,000*2%=400组合每日的波动=(100^2+400^2+2×100×400×0.3)^0.5=440.55天97%的VAR=440.5*(5)^0.5*1.88=1852.4 U 减去Z 乘波动公式不能适用吗？和例题一样啊。反而解题公式没看到过。请详细说说。为啥不能用讲义上的公式，十分困惑。多谢

2023-03-11 15:01 2 · 回答