B是啥意思，可以解释一下吗

问题如下：

The CRO of a regional bank expresses concern in a risk team meeting that the bank’s internal risk models are not adequate in assessing potential random extreme losses. A risk analyst suggests that implementing a model based on extreme value theory (EVT) could address this concern. Which of the following is correct when applying EVT and examining distributions of losses exceeding a threshold value?

选项：

A.As the threshold value is increased, the distribution of losses over a fixed threshold value converges to a generalized Pareto distribution.

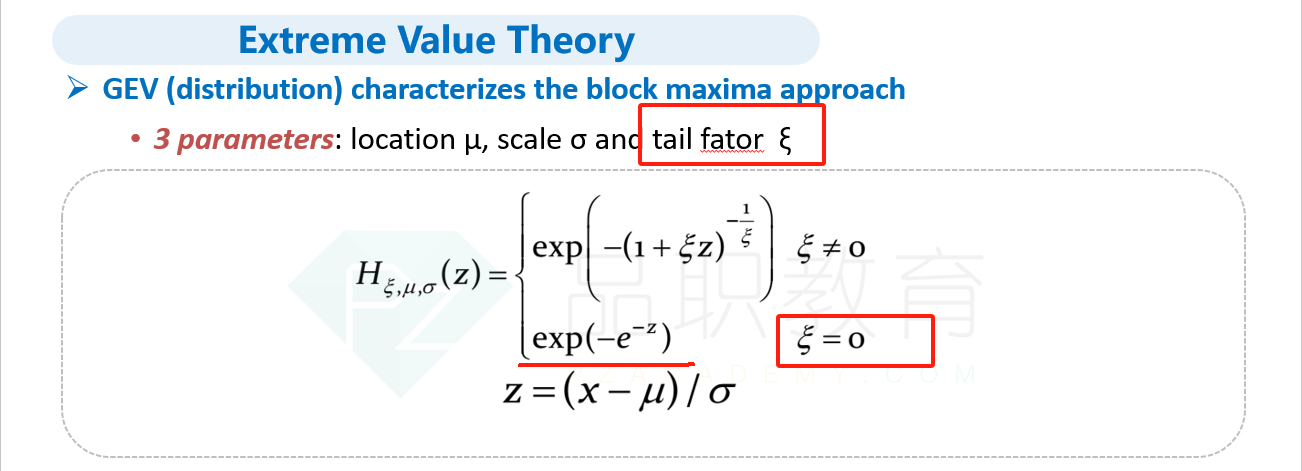
B.If the tail parameter value of the generalized extreme-value (GEV) distribution goes to infinity, then the GEV essentially becomes a normal distribution.

C.To apply EVT, the underlying loss distribution must be either normal or lognormal.

D.The number of exceedances decreases as the threshold value decreases, which causes the reliability of the parameter estimates to increase.

解释：

A is correct. A key foundation of EVT is that as the threshold value is increased, the distribution of loss exceedances converges to a generalized Pareto distribution. Assuming the threshold is high enough, excess losses can be modeled using the generalized Pareto distribution. It is known as the Gnedenko–Pickands–Balkema–deHaan (GPBdH) theorem and is heavily used in the peaks-over-threshold (POT) approach. B is incorrect. If the tail parameter value of the generalized extreme-value (GEV) distribution goes to zero, and not infinity, then the distribution of the original data (not the GEV) could be a light-tail distribution such as normal or log-normal. In other words, the corresponding GEV distribution is a Gumbel distribution. C is incorrect. To apply EVT, the underlying loss distribution can be any of the commonly used distributions: normal, lognormal, t, etc. D is incorrect. As the threshold value is decreased, the number of exceedances increases.