NO.PZ2023100703000073
问题如下:
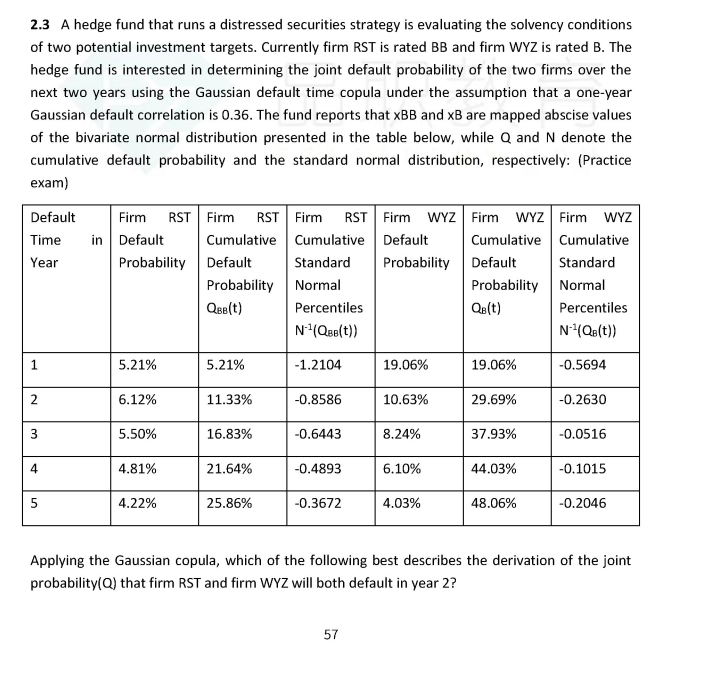
A hedge fund that runs a distressed securities strategy is evaluating the solvency conditions of two potential investment targets. Currently firm RST is rated BB and firm WYZ is rated B. The hedge fund is interested in determining the joint default probability of the two firms over the next two years using the Gaussian default time copula under the assumption that a one-year Gaussian default correlation is 0.36. The fund reports that xBB and xB are mapped abscise values of the bivariate normal distribution presented in the table below, while Q and N denote the cumulative default probability and the standard normal distribution, respectively:

Applying the Gaussian copula, which of the following best describes
the derivation of the joint probability(Q) that firm RST and firm WYZ will both
default in year 2?
选项:
A.Q(xBB = 0.0612) + Q(xB = 0.1063) – Q(xBB = 0.0612)*Q(xB = 0.1063) B.Q(xBB = 0.1133) + Q(xB = 0.2969) – Q(xBB = 0.1133)*Q(xB = 0.2969) C.Q(xBB≤0.1133∩xB≤0.2969) D.Q(xBB ≤-0.8586∩xB≤-0.2630)解释:
The joint probability of default is measured by “cumulative standard normal percentiles.” What the copula function does is to: first, map the cumulative default probability values (marginal distributions) of a multivariate distribution - percentile to percentile - to a cumulative standard normal distribution. Then, second, find the mapped abscise (x-axis) values of the cumulative standard normal distribution. The Gaussian copula procedure essentially assumes that only a single correlation (not a correlation matrix) can now be applied to the multivariate distribution.题干表格少了最后一列的信息。