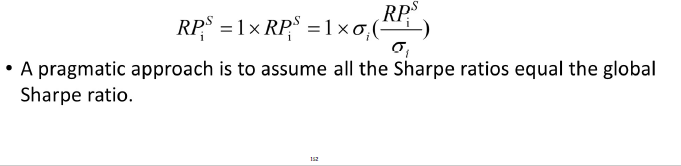NO.PZ2022122601000061
问题如下:
Étienne Leroy is a global investment strategist for a French investment advisory firm. He is currently reviewing the asset allocation of the firm’s largest global fund. Leroy estimates the expected returns for three asset classes: North American equities, Eurozone fixed income, and Asia-Pacific real estate. He uses the Singer-Terhaar approach to the international capital asset pricing model for his analysis. Leroy gathers data for each asset class as shown in Exhibit 1.
Leroy makes the following assumptions in his analysis:
The expected return for the GIM is 6.0%.
The expected standard deviation for the GIM is 12.5%.
The risk-free interest rate is 2.0%.
The Asia-Pacific real estate asset class has an illiquidity premium of 0.4%.
A. Calculate the expected return for the Asia-Pacific real estate asset class, using the Singer-Terhaar approach. Show your calculations.
选项:
解释:
Correct Answer:
Most markets lie between the extremes of perfect market integration and complete market segmentation.
For perfect integration, the expected risk premium of an asset is expressed as: [(σi) x (ρi, M) x (Sharpe ratio GIM)] + Illiquidity premium
For complete segmentation, the expected risk premium of an asset is expressed as: [(σi) x Sharpe ratio GIM)] + Illiquidity premium
where: σi is the standard deviation or volatility of the asset’s returns ρi, M is the correlation of the asset’s returns with the Global Investable Market’s (GIM) returns
The answer calculated as follows:
1. Determine the Sharpe ratio of the GIM: RPM / σM = (6% – 2%) / 12.5% = 0.32
where: RPM is the risk premium of the GIM
σM is the standard deviation or volatility of the GIM’s returns
2. Calculate the Asia-Pacific real estate risk premium under the assumption of perfect integration (see formula above): [13% x 0.47 x 0.32] + 0.4% = 2.36%
3.
Calculate the Asia-Pacific real
estate risk premium under the assumption of complete segmentation (see formula
above): [13% x 0.32] + 0.4% = 4.56%
4. Calculate the weighted average of the risk premiums based on a 60% degree of market integration: [2.36% x 0.60] + [4.56% x 0.40] = 3.24%
5. The expected return on an investment in Asia-Pacific real estate equals the risk-free interest rate plus the weighted average of the risk premiums = 2.0% + 3.24% = 5.24%.
中文解析:
大多数市场处于完全的市场整合和完全的市场细分这两个极端之间。
对于完美整合,资产的预期风险溢价表示为:[(σi) x (ρi, M) x(夏普比率GIM)] +非流动性溢价
对于完全分割,资产的预期风险溢价表示为:[(σi) x夏普比率GIM)] +非流动性溢价
式中:σi为资产收益的标准差或波动性,ρi, M为资产收益与全球可投资市场(Global Investable Market, GIM)收益的相关性
答案计算如下:
1. 确定GIM的夏普比率:RPM / σM = (6% - 2%) / 12.5% = 0.32
式中:RPM为GIM的风险溢价
σM是GIM收益的标准差或波动性
2. 在完全整合假设下计算亚太房地产风险溢价(见上式):[13% x 0.47 x 0.32] + 0.4% = 2.36%
3.计算完全分割假设下亚太房地产风险溢价(见上式):[13% x 0.32] + 0.4% = 4.56%
4. 根据60%的市场一体化程度计算风险溢价的加权平均值:[2.36% x 0.60] + [4.56% x 0.40] = 3.24%
5. 亚太地区房地产投资的预期收益=无风险利率加上风险溢价的加权平均值= 2.0% + 3.24% = 5.24%。
完全分割假设下不应该是去计算当前资产的return premium吗?为什么这里是计算的GIM的reterm premium(correlation=1的情况)