老师,这道题的算法我有点不太明白:
第一步算的是△y的最大值,那么用正态分布和VaR来求△y最大值,是否应该是△y服从正态分布,△y均值为零,用u+2.33*sigma(△y)来计算?
但是题目已知的是return服从正态分布,以及yield volatility(sigma y)
发亮_品职助教 · 2024年07月02日
第一步算的是△y的最大值,那么用正态分布和VaR来求△y最大值,是否应该是△y服从正态分布,△y均值为零,用u+2.33*sigma(△y)来计算?
还不是,这是一个套路题型。都是已知YTM服从正态分布,并非债券价格的波动幅度△y。当然,如果更进一步讨论的话,债券价格的波动幅度△y也是服从正态分布的,确实可以用提问说的方法算VaR。但是这个题型的标准算法就是这道题答案给的。
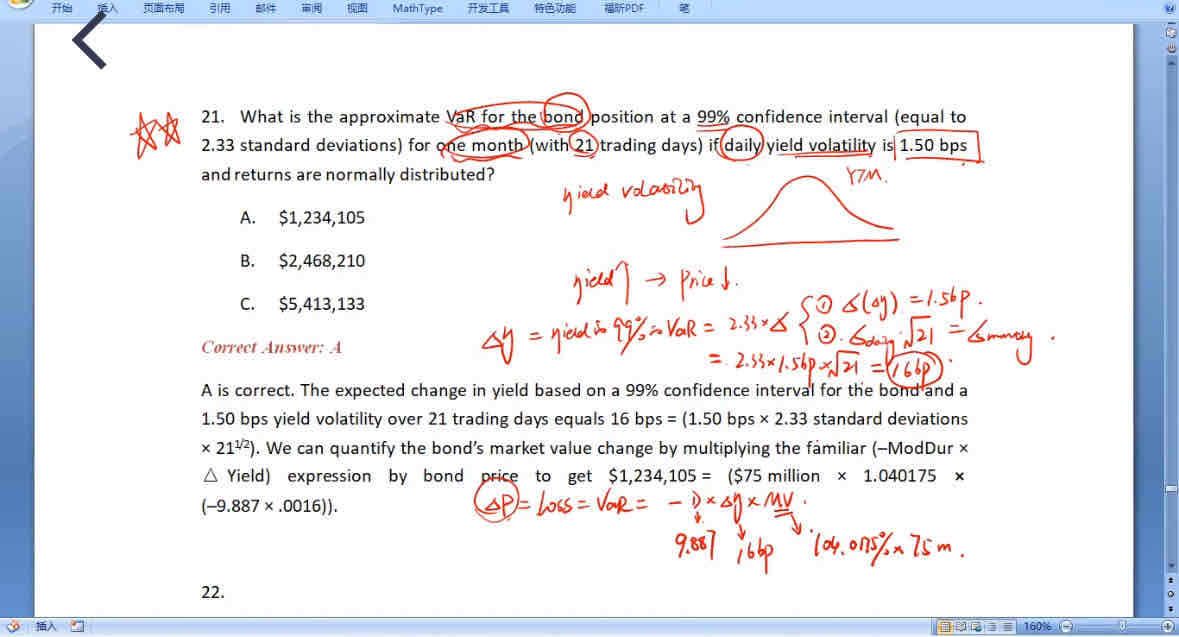
做题的步骤是:
已知YTM的分布 → 算YTM的VaR值 → 再乘以Duration算出来债券价格波动的VaR值 → 再乘以债券的Market value算债券价格的VaR值
首先要利用YTM的分布找到△YTM的分界点VaR值,算法就是μ+2.33×sigma,已知均值μ为0,而Sigma必须是要把每天的sigma转换成题目待求的每月sigma:
daily sigma×根号21天 = 1.50bps × 根号21天 = 6.8739 bps = 0.0687%
μ+2.33×sigma = 0 + 2.33 × 0.0687% = 0.1602%,这个0.1602%是△YTM的99% VaR,意思是99%的概率下,YTM的最大涨幅
然后再利用债券价格和YTM之间的关系,给△YTM的VaR值乘以duration可以算出来债券价格最大变动幅度VaR值:
-duration × △YTM VaR = - 9.887 × 0.1602% = -1.5835%
可知,99%的概率下,债券价格下降幅度最大为(99%的债券价格VaR):-1.5835%
然后再乘以债券的Market value,可以算出来债券价格的变动VaR值:
-1.5835% × 75 million × 104.0175% ≈ 1235338 (和答案的出入主要是四舍五入的误差)
其中75 million是债券的面值,104.0175%是债券的报价,75 million×104.0175%是债券的市场价格market value
但是题目已知的是return服从正态分布,以及yield volatility(sigma y)
是的,这个套路的题型都是这样哈,要按照上面的步骤算。
cherry0540 · 2024年07月02日
如果题目告诉了YTM的值,在u+2.33*sigma(△y)中要带入u吗?
发亮_品职助教 · 2024年07月02日
这个有2种算法。具体看yield volatility的大小。如果Yield volatility比较大,如1.5%,0.8%这种带有百分号的,算VaR时需要再乘以YTM缩小数据,μ+2.33×σ,已知均值为0,所以为2.33σ,但算σ的时候,需要用yield volatility再乘以YTM。如果yield volatility比较小,如果1.5bps,0.8bps,5bps,这种就不要再乘YTM了。不过现在从协会出的题以及25年新教材来看,不乘YTM的概率会比较大。