NO.PZ2020021205000058
问题如下:
A stock price is currently 50. Its volatility is 20% per annum. The risk-free rate is 4% per annum with continuous compounding. value an option that pays off max( - 2,400, 0) in six months where S is the stock price. (This is known as a power option.)
解释:
For the power option, the tree becomes as follows, and the value of the option is 408.363.
解析:
power option是一种奇异期权叫做幂期权,他与一般的期权的区别在于,在T时刻,看涨幂期权的价值=max{0,Sn -X},而不是max{0,S-X}。该期权简单了解即可。
对于本题的这个幂期权,其价值=max{S2 -X,0}。具体的二叉树如下:
1、老师好,这道题的u(p)和d(1-p)分别是多少啊?
2、红色方框是前往前折现再乘以对应的概率吗?
3、折现的利率,折现到0.25段儿是4%乘以0.25,去年化?
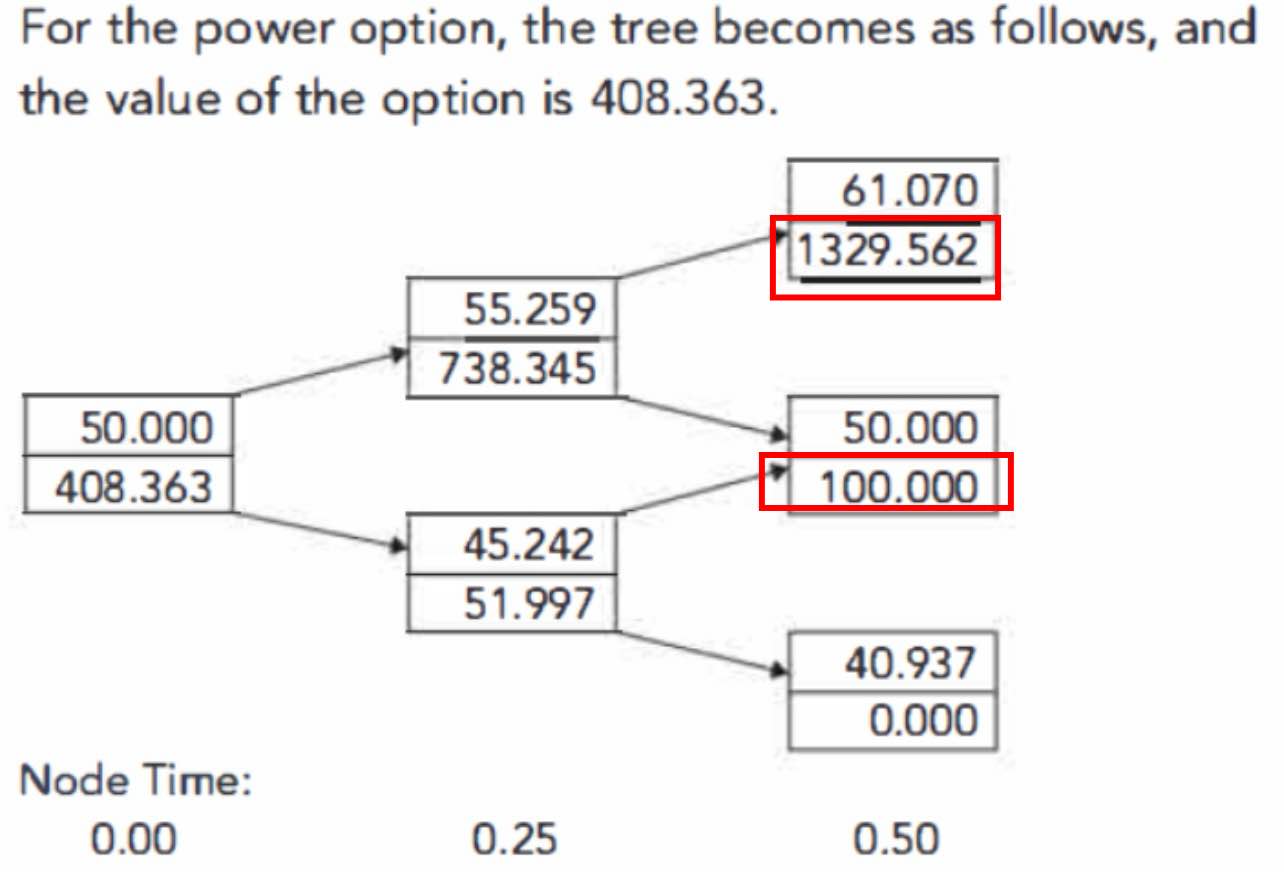
我计算两个红色方框折现再乘以概率是744,不是738耶
4、标准差20%也要去年化吗?还是20%*0.25^0.5就行?




