
老师好,我较少时间看视频,主要是复习之前记录下来的PPT。请看图2,为什么图2中有那么多的×?? 意思是答案是错误的吗?那正确的答案应该是怎么样的?
发亮_品职助教 · 2024年06月21日
这道题主要是折现率用的有点问题。
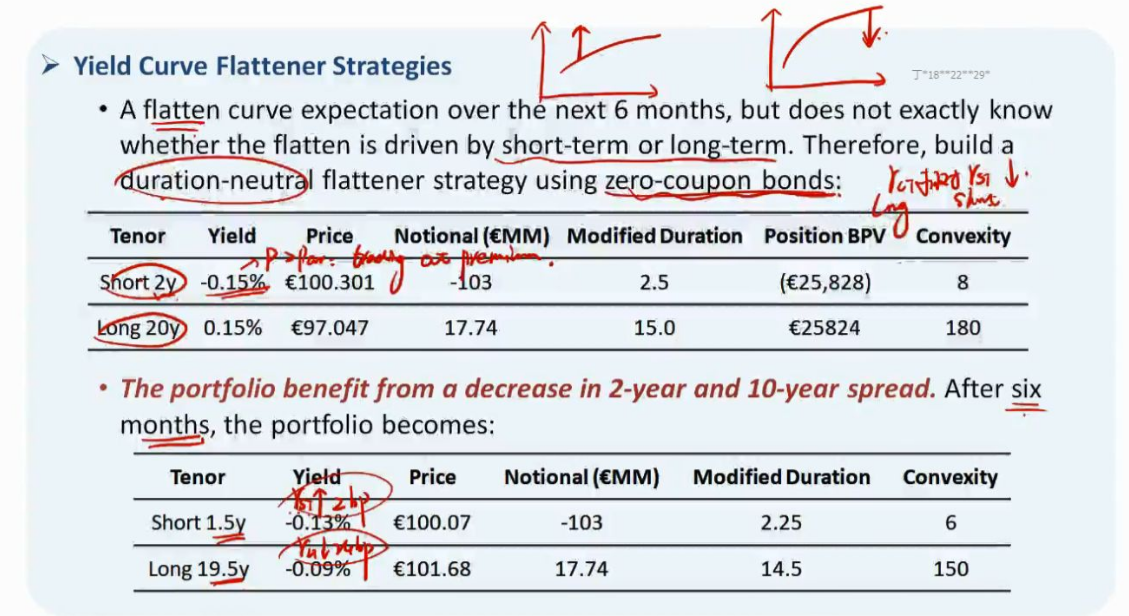
最右边的叉号是这样,这个公式是在计算利率曲线移动带来的价差,原版书在算价格时,分别用了-0.15%和0.15%进行折现。而-0.15%是2年期的利率,0.15%是20年期利率。不应该用这两个利率。应该用1.5年期和19.5年期的利率。
债券的价差由2部分构成,一部分是债券期限缩短,在stable yield curve上roll down的价差,这里体现时间差异带来的价差,不含利率曲线移动的价差。
第2部分是利率曲线移动带来的价差,这里体现利率曲线移动的价差,不含时间差异带来的价差。讲义这个计算式子其实是在计算第2部分价差。
恰好本题利率波动了,所以肯定有这2部分价差。
其中stable yield curve上rolldown的价差,第1个债券期初价折现用2-year利率,期末价折现用stable curve上的1.5年期利率;第2个债券期初价折现用20年期利率,期末价折现用stable curve上的19.5年期利率。
而在计算利率波动的价差时,第1个债券利率改变前的价格应该用stable curve上的1.5年期折现率,改变后的价格应该用利率波动后的新1.5年期折现率;第2个债券利率改变前的价格应该用stable curve上的19.5年期折现率,改变后的价格应该用利率波动后的新19.5年期折现率。而我们教材在计算这部分价差时,利率改变前的价格用的仍然是20年和2年期利率折现,所以有错。
如果用20年期和2年期的折现率算期初价格,期末价格用利率波动之后的折现率。那这个价差其实包含两部分价差:既包含从20年rolldown至19.5年的价差(从2年rolldown至1.5年的价差),又包含在stable curve19.5年利率的基础上,利率再移动的价差(在stable curve 1.5年利率的基础上,利率再移动的价差)
因为这里面前后的折现率既体现了期限的差异,又体现了波动的差异。
这出现了重复计算,因为roll down return我们在上面已经计算过了,这块就单纯地想计算利率波动带来的价差。
所以,单纯地要计算利率移动的价差,应该用利率移动后19.5年期和1.5年期的利率算期末价格,用利率移动前的stable curve上19.5年期和1.5年期的利率算期初价格,这里只体现利率移动,不含期间改变带来的差异。而教材却用了20年期的-0.15%和0.15%,所以这里错误。
最左边这个叉号是说,其实教材这块多此一举了,计算利率改变带来的价差时,直接用duration和convexity近似算就行了,这也是我们一般的算法,不需要分别折现算期初、期末的价格