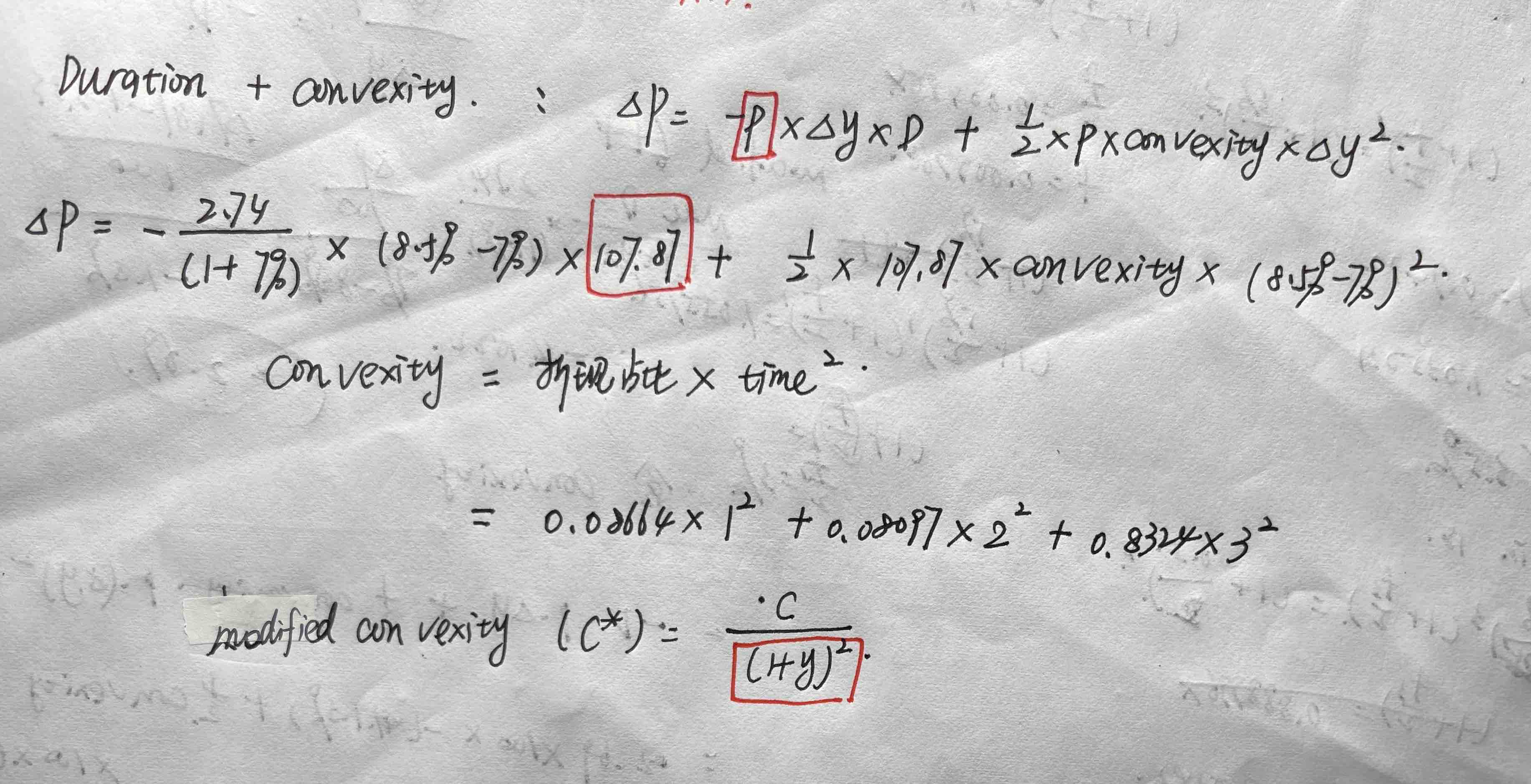NO.PZ2020021204000019
问题如下:
A three-year bond with a face value of USD 100 pays coupons annually at the rate of 10% per year. Its yield is 7% with annual compounding., estimate the price change if the annually compounded yield changes from 7% to 8.5%, using both the duration and the duration plus convexity approximations.
解释:
Using duration, the price change is
-2.5661 X 107.8729 X 0.015= -4.1522
Using duration and convexity, it is
-2.5661 X 107.8729 X 0.015 + (1/2) X 6.9020 X 107.8729 X 0.0152 = -4.0685
The actual bond price decline is 4.0419, showing that duration plus convexity gives a better estimate than convexity alone.
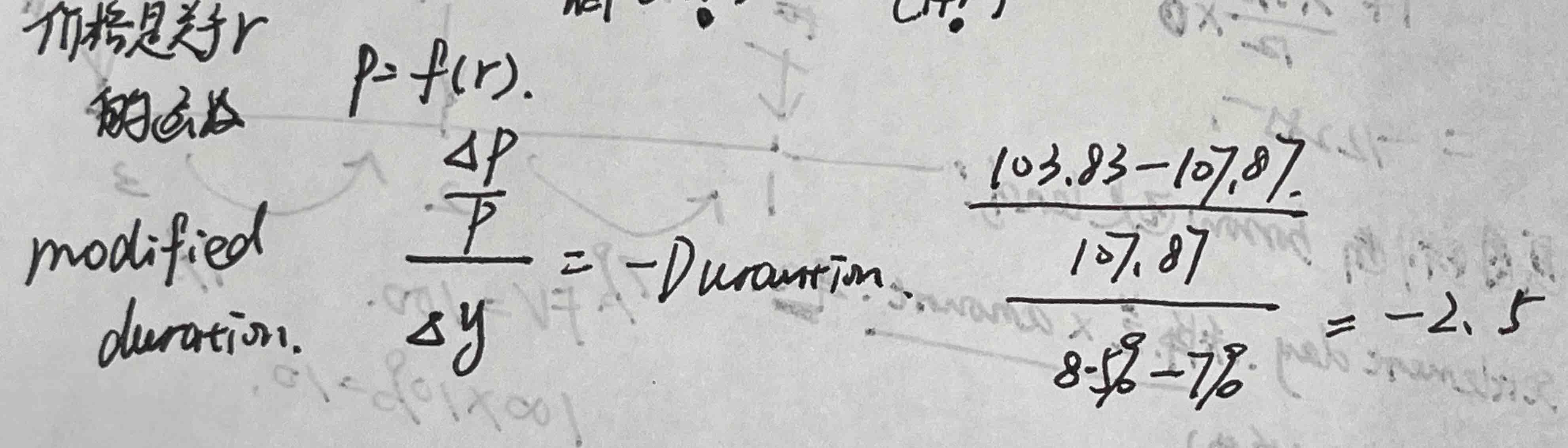
不用modified duration=macaulay duration/(1+y)行不行?就用modified的定义式:deta p=-Duration*得塔y*p?得出结果是-2.5,与用modified 和macaulay的关系式求解的结果有少许差异。

感觉这张图求convexity不太对吧?第一个蓝框
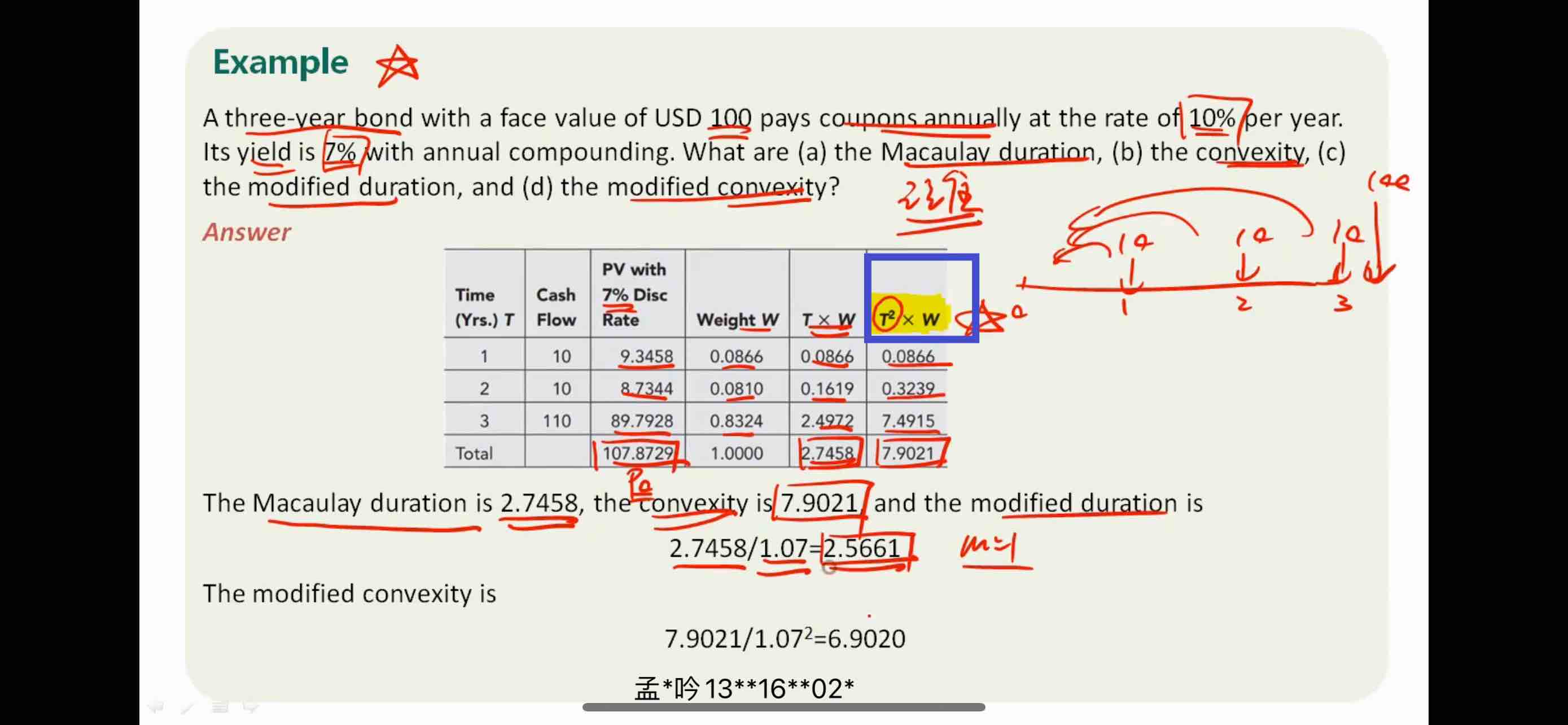
您看课程例题的截图,不应该是权重(即现金流折现占现值比例)乘以时间的平方吗?如下图我写的0.08664*1+0.08097*4+0.8324*9吗?