NO.PZ2022123002000003
问题如下：
Pete Aron, portfolio
manager for Gulf & Co.’s European technology fund, is concerned about
currency fluctuations related to the equity portfolio (the Portfolio). The
Portfolio is valued in USD, but has exposure to multiple European currencies,
primarily the EUR.
Aron formulates
the following market expectations for the coming year:
The market quotes
presented in Exhibit 1 are available from a currency dealer:
Aron considers
selling EUR and buying USD using a one-year forward contract to fully hedge the
EUR currency risk. He will execute the trade if he can achieve the following
risk/return objectives:
Objective 1: Increase the Portfolio’s expected return
(in USD) by at least 25 basis points.
Objective 2: Reduce the Portfolio’s expected standard deviation (in USD) by at least 30 basis points.
Determine, based
on Aron’s market expectations, whether he should execute the forward trade with
respect to each of the following:
i. Objective 1
ii. Objective 2
Justify your
response. Show your calculations. (2015 Q9)
Note: Assume a
one-year time horizon. Consider each objective independently.
选项：
解释：
Correct Answer:
Objective 1:
Aron should not
execute the forward trade because the return objective is not met.
For the USD-based
investor, the expected USD return on the USD/EUR is 1.2045/1.1930 – 1 = 0.96%.
Since the EUR return on the portfolio is given at 13.2%, the unhedged USD
return on the portfolio is calculated as (1 + 0.96%)(1 + 13.2%) – 1 = 14.29%.
If Aron decides to
hedge by selling EUR forward, the return on the USD/EUR will be 1.2065/1.1930 –
1 = 1.13% and the return on the hedged portfolio would be (1 + 1.13%)(1 +
13.2%) – 1 = 14.48%.
The difference
between the hedged return and the unhedged return is 14.48% – 14.29% = 19 bps,
which is less than Aron’s required additional return of 25 bps.
Alternatively, one
could calculate the difference between the hedged and unhedged return and get
(1 + 14.48%)/(1 + 14.29%) – 1 = 17 bps, which is also less than Aron’s required
return.
Objective 2:
Aron should
execute the forward trade because the risk objective is met.
If Aron does not
execute the trade, the expected unhedged domestic-currency standard deviation
is calculated as follows; note that the USD is the domestic currency and the
EUR is the foreign currency:
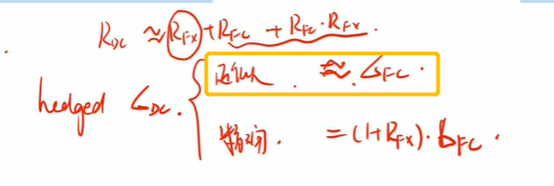
Taking the square
root of 0.02395 gives σ(RDC) = 15.48%. If Aron executes the trade,
the expected USD portfolio standard deviation equals the standard deviation of
the EUR equity position, 15.00%. Therefore, the standard deviation of the
portfolio decreases by 15.48% – 15.00% = 48 bps, which is more than Aron’s
required decrease of 30 bps.
第二问为什么不是σ（RDC）=(RFX+1)*σ（RFC)？记得上课中提到hedged的情况下要这么算，跟答案直接σ（RDC）=σ（RFC)不一样
