NO.PZ2020012005000040
问题如下:
Suppose that F1 and F2 are the futures prices on the same commodity with maturities t1 and t2 with t2 > t1. Storage costs are negligible. The risk-free rate is R for all maturities. Use an arbitrage argument to show that:
解释:
A trader can enter into a long futures contract with maturity t1 and a short futures contract with maturity t2. At time t1 F1 is borrowed and the asset is bought for F1. The loan is repaid at time t2 and the asset is sold for F2.
The cash flows are
Time , and
Time
This simple strategy is certain to lead to a profit at time t2 if:
Thus, the prices will adjust such that:

这道题思路的出发点就没懂,怎么想到要借F1,买F1资产,而不是F2?为什呢不是从0时刻开始,而是从t1时刻开始?t1时刻建立的空头期货就是F2吗?能否画个图说一下这种题怎么想?




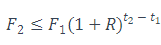 ,
,