Correlation diversification

嗨，从没放弃的小努力你好：

只要correlation小于1就有分散效果吗，为什么不是小于0呢？

是的，只要小于+1就是有分散化的效果。当然越小越好，越小分散化效果越强。极限就是correlation等于-1时，分散化的效果最强。

为什么是小于1就会有分散化效果？

假设两个资产的correlation等于1，这时候意味着当A资产的价格上涨时，B资产也是100%上涨的，当A资产的价格下跌时，B资产的价格也100%一定是下跌的，且两者的变动比例恒定，两者总是同涨同跌。

两个资产同涨同跌就可以看成是一个资产。一个资产肯定没有分散化效果。

但如果Correlation小于1，这时候说明两个资产的价格波动方向不是100%同涨同跌的，有可能出现反向变化，如当A资产的价格上升时，B资产的价格有可能会下跌，B的下跌会被A的上升弥补住一部分，这会使得整体组合的亏损幅度下降。这就是分散化的效果。

考虑公式的话是这样，假设组合由A、B两个资产构成，A在组合内的权重是wA，B在组合内的权重是wB，A的标准差是σA，B的标准差是σB，两者的相关系数是ρ，已知组合的方差公式：

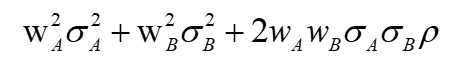
假设ρ等于1，两个资产完全相关，ρ代入1，则上面的式子变成：

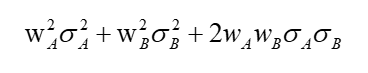
这就是初中学过的完全平方和公式，他等于：

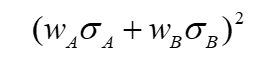
开平方后就得到标准差，即组合的风险：

组合的风险 = wA×σA + wB×σB

这说明，当两个资产间的相关系数为+1时，把这两个资产组合到一起，组合的风险就是两个资产各自风险的加权平均，就是各自的权重乘以各自的风险进行加总，其本质就是把2个资产的风险加总形成组合风险，只不过是考虑了权重，这说明此时没有分散化的效果。

但只要假设correlation < 1

组合的方差公式为：

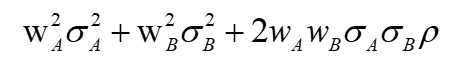
以上这个公式算出来的数值，肯定小于当ρ=1时的数值，因为ρ取1时为最大值，取1时第3项2wA×wB×σA×σB×ρ最大，只要ρ小于1，第三项就开始变小。

所以当ρ小于1时，组合的方差小于ρ等于1时的组合方差，可以列出下面式子：

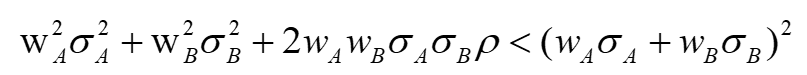
其中，不等号左边是ρ小于1的组合方差，不等号右边是ρ等于1时组合的方差

这说明，当ρ小于1时，把两个资产组合到一起，此时组合的风险就开始小于两个资产风险的直接加总（加权平均），说明当ρ小于1，两者有一定风险的抵消作用了，所以才开始导致组合的风险小于组合内2个资产风险的直接加总（加权）

且可以看出ρ越小，第三项越小，不等号左边数值越小，说明把两个资产组合到一起后的风险越小，分散化的效果越好。

当ρ=0时的分散化肯定还要更好，比0<ρ<1的分散化效果好

当-1<ρ<0时，correlation是负数时，分散化效果还要进一步提升，极限就是ρ=-1时分散化的效果最好。

还有FI equity经常会考什么加入某种资产整体怎么变？

就看资产和原来Portfolio之间的correlation大小，只要小于1，加入这个资产后会进一步降低组合风险，correlation越小分散化效果越好。

同时还要看这个资产和原portfolio的标准差大小，如果这个资产的标准差比原portfolio还要小，那加入这个资产之后会进一步降低组合的风险。

是不是加入Rf也不一定方差减小？

一定会让组合的风险、方差进一步减小。因为Rf首先是无风险，他的标准差是0，组合原来的标准差肯定大于0，当把Rf加到组合里时，Rf的0标准差/方差和原来组合的标准差/方差做加权平均算新标准差/方差，那肯定会进一步拉低原Portfolio的标准差/方差。

同时Rf和所有其他资产的correlation默认是0，这个correlation很小了。

加入高风险的也不一定风险增大？

是的，加入高风险不一定使得组合风险变大，因为还要看资产和原组合之间的correlation大小。

或者说资产对组合风险的影响取决于2点，一个是资产自身的风险大小，一个是资产与组合的correlation

这里还需要掌握什么呢？

应该没有了，三级已经不太考这些点了，基本最常见到的就是ρ<1可以起到分散化

----------------------------------------------
就算太阳没有迎着我们而来，我们正在朝着它而去，加油！