这道例题重要吗？

嗨，努力学习的PZer你好：

例题本身不重要，里面展示的信息是比较重要的，差不多就是你列的这些点。

如提问所说，这道例题展示了Cash flow yield是债券Portfolio的YTM/IRR

同时，债券期间的现金流再投资利率就是Cash flow yield

另外发现，当负债到期时，Portfolio里面的现金流呈现不同状态：

期限短的、提前到期的现金流，必须要以Cash flow yield进行再投资，直至负债到期；

而期限长的、尚未到期的现金流，必须要提前卖掉/以Cash flow yield折现到负债到期算PV，在负债到期时卖出。

在负债到期时刻，以上两股现金流汇总（Coupon与再投现金流 + 提前卖出债券回收的现金流）才是真正偿还负债的现金流。

这道题也展示了Macalauy duration的精确计算方法，就是给Portfolio里面的每一期现金流发生的时间做加权平均；也展示粗略的计算方法，就是给Portfolio里面的成份债券的Macaulay duration算加权平均。

也展示了2个公式，分别是Macaulay duration、Dispersion与Conveixty的关系，以及期限t与convexity之间的关系，定性关系及公式要记一下。

这道例题展示的内容基本如上

Time 5的现金流就是发生在这个时刻的Coupon以及本金现金流加总，由于本题的债券是半年付息一次，所以1单位time对应的是0.5年，于是time 5对应的是2.5年年末。

在time 5时刻的现金流有4笔：3个债券的coupon，以及第一支2.5年期债券到期的本金。

三个债券的coupon为：

第一支债券每期Coupon：47,000,000×1.5%×0.5 = 352500

第二支债券每期Coupon：97,300,000×3.25%×0.5 = 1581125

第三支债券每期Coupon：55,600,000×5%×0.5 = 1390000

加总是：352500 + 1581125 + 1390000 = 3323625

加上第一支债券的到期本金是：3323625 + 47,000,000 = 50323625

----------------------------------------------
加油吧，让我们一起遇见更好的自己！

嗨，爱思考的PZer你好：

这个的话，是因为convexity是second-order derivatives, 而duration都是first-order derivatives. 对吧? 不过，这个点会考吗？或者说，如果考的话，会怎么考?

是的，Duration一阶导，Convexity二阶导

导数关系基本不太考。考的话基本只见过时间t和convexity的关系是平方，债券期限涨一点点，convexity会大幅度上涨。

----------------------------------------------
就算太阳没有迎着我们而来，我们正在朝着它而去，加油！

嗨，努力学习的PZer你好：

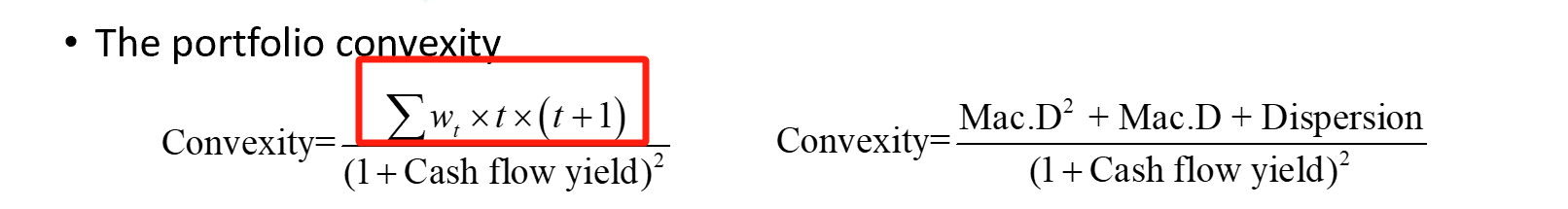
就是第一个公式。结论就是convexity和债券的期限（t）成平方的关系，债券的期限变动一点会导致convexity发生更剧烈的改变（和Macaulay duration/Modified duration等Duration数据相比）

比如，零息债券的期限由3上涨到了9，Macaulay duration简单来看由3上涨到了9，上涨幅度是3倍；但是因为Convexity与t呈现平方关系，convexity上涨的幅度是9倍。

就这一个定性关系。计算的话后面Macaulay duration和Convexity是相对更容易出计算。

----------------------------------------------
努力的时光都是限量版，加油！