NO.PZ2018123101000109
问题如下:
Lebedeva asks Kowalski to analyze a three-year bond, issued by VraiRive S.A., using an arbitrage-free framework. The bond’s coupon rate is 5%, with interest paid annually and a par value of 100. In her analysis, she makes the following three assumptions:
■ The annual interest rate volatility is 10%.
■ The recovery rate is one-third of the exposure each period.
■ The hazard rate, or conditional probability of default each year, is 2.00%.
Selected information on benchmark government bonds for the VraiRive bond is presented in Exhibit 2, and the relevant binomial interest rate tree is presented in Exhibit 3.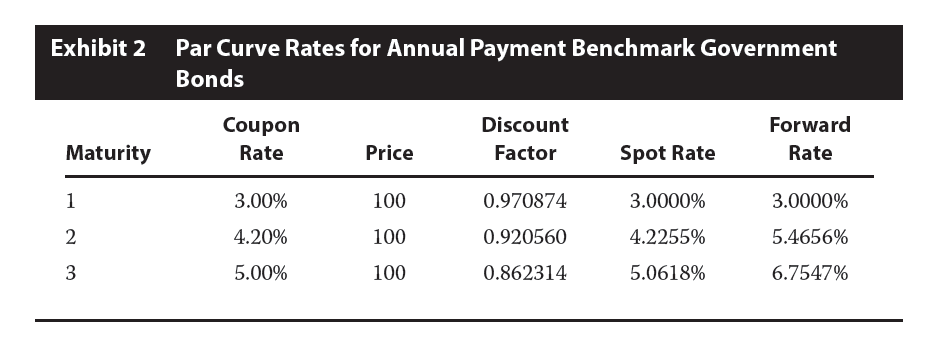

Based on Kowalski’s assumptions and Exhibits 2 and 3, the credit spread on the VraiRive bond is closest to:
选项:
A.
0.6949%.
B.
0.9388%.
C.
1.4082%.
解释:
C is correct. The credit spread can be calculated in three steps:
Step 1 Estimate the value of the three-year VraiRive bond assuming no default. Based on Kowalski’s assumptions and Exhibits 2 and 3, the value of the three-year VraiRive bond assuming no default is 100.0000.
Supporting calculations:
The bond value in each node is the value of next period’s cash flows discounted by the forward rate. For the three nodes on Date 2, the bond values are as follows:
105/1.081823 = 97.0584.
105/1.066991 = 98.4076.
105/1.054848 = 99.5404.
For the two nodes on Date 1, the two bond values are as follows:
[0.5 × (97.0584) + 0.5 × (98.4076) + 5.00]/1.060139 = 96.9052.
[0.5 × (98.4076) + 0.5 × (99.5404) + 5.00]/1.049238 = 99.0948.
Finally, for the node on Date 0, the bond value is
[0.5 × (96.9052) + 0.5 × (99.0948) + 5.00]/1.030000 = 100.0000.
Therefore, the VND for the VraiRive bond is 100.0000.
Step 2 Calculate the credit valuation adjustment (CVA), and then subtract the CVA from the VND from Step 1 to establish the fair value of the bond. The CVA equals the sum of the present values of each year’s expected loss and is calculated as follows:
Supporting calculations:
The expected exposures at each date are the bond values at each node, weighted by their risk-neutral probabilities, plus the coupon payment:
Date 1: 0.5 × (96.9052) + 0.5 × (99.0948) + 5.00 = 103.0000.
Date 2: 0.25 × (97.0584) + 0.5 × (98.4076) + 0.25 × (99.5404) + 5.00 = 103.3535.
Date 3: 105.0000
The loss given default (LGD) on each date is 2/3 of the expected exposure.
The probability of default (POD) on each date is as follows:
Date 1: 2%
Date 2: 2% × (100% – 2%) = 1.96%.
Date 3: 2% × (100% – 2%)2 = 1.9208%.
The discount factor on each date is 1/(1 + spot rate for the date) raised to the correct power.
Finally, the credit valuation adjustment each year is the product of the LGD times the POD times the discount factor, as shown in the last column of the table. The sum of the three annual CVAs is 3.7360.
So, the fair value of the VraiRive bond is the VND less the CVA, or VND – CVA = 100 – 3.7360 = 96.2640.
Step 3 Based on the fair value from Step 2, calculate the yield to maturity of the bond, and solve for the credit spread by subtracting the yield to maturity on the benchmark bond from the yield to maturity on the VraiRive bond. The credit spread is equal to the yield to maturity on the VraiRive bond minus the yield to maturity on the three-year benchmark bond (which is 5.0000%). Based on its fair value of 96.2640, the VraiRive bond’s yield to maturity (YTM) is
96.2640=5/(1+YTM)+5/(1+YTM)2+105/(1+YTM)3
Solving for YTM, the yield to maturity is 6.4082%. Therefore, the credit spread on the VraiRive bond is 6.4082% – 5.0000% = 1.4082%.
想问下求解spread的bech rate 用的是同期限的par rate吗,为什么不用spot rate



