NO.PZ202305230100005304
问题如下:
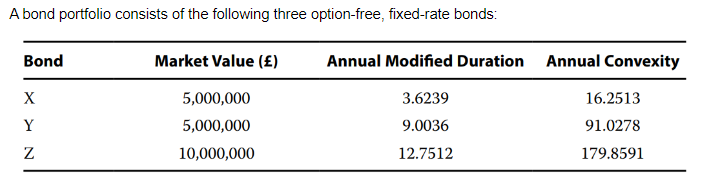
For a 100 bps increase in yield-to-maturity and using the weighted average duration and convexity, the expected percentage price change for the bond portfolio is closest to:
选项:
A.–7.981%
–8.949%
–9.533%
解释:
B is correct. The portfolio weights for Bonds X, Y, and Z are 0.25, 0.25, and 0.50, respectively. The weighted average duration and convexity measures are calculated as follows:
Weighted-average duration = (0.25 × 3.6239) + (0.25 × 9.0036) + (0.50 × 12.7512) = 9.5325.
Weighted-average convexity = (0.25 × 16.2513) + (0.25 × 91.0278) + (0.50 × 179.8591) = 116.7493.
%ΔPVFull ≈ (–9.5325 × 0.01) + [0.5 × 116.7493 × (0.01)^2]
= –8.9487% ≈ –8.949%.
感觉这道题的算法很复杂,考试会考这么复杂的算术题吗?