NO.PZ2023091802000209
问题如下:
An options trader is applying the Black-Scholes-Merton option pricing model to estimate the delta of a long 1-year European put option on a dividend-paying stock. Relevant data is provided below:
· Annual continuously compounded risk-free rate of interest: 2.0%
· Annual dividend yield on the stock: 3.5%
· N(d1): 0.5411
· N(d2): 0.4287
What is the delta of the put option?
选项:
A.−0.5517
−0.5411
−0.4589
−0.4431
解释:
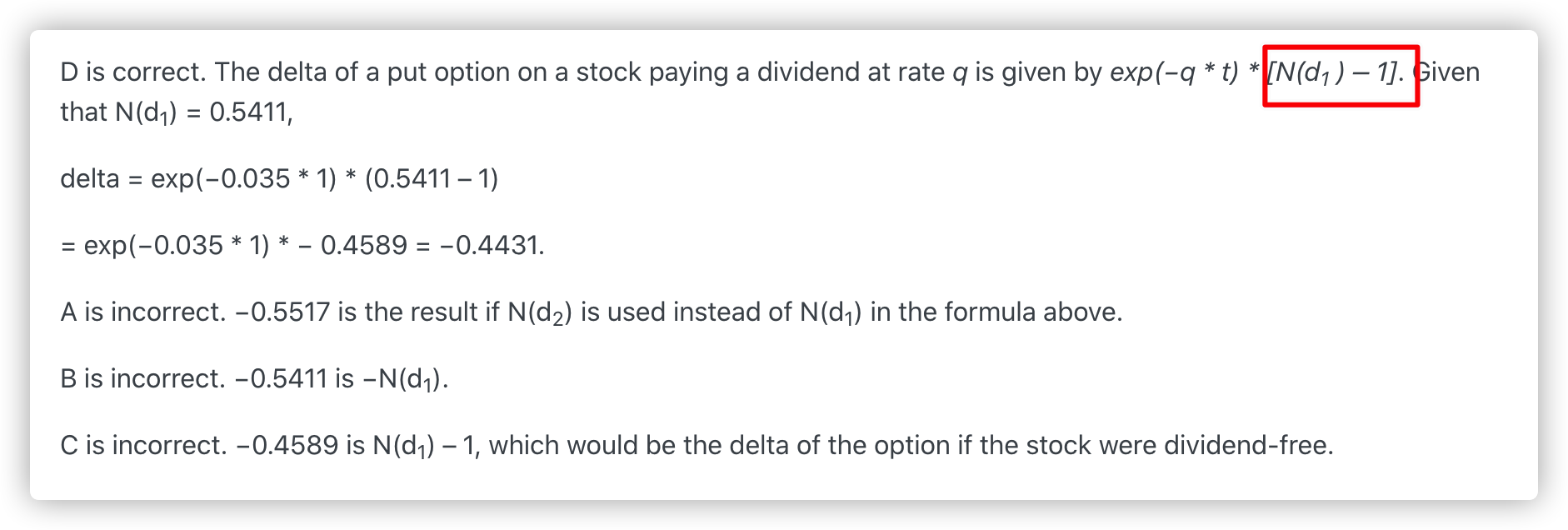
D is correct. The delta of a put option on a stock paying a dividend at rate q is given by exp(−q * t) * [N(d1 ) – 1]. Given that N(d1) = 0.5411,
delta = exp(−0.035 * 1) * (0.5411 – 1)
= exp(−0.035 * 1) * − 0.4589 = −0.4431.
A is incorrect. −0.5517 is the result if N(d2) is used instead of N(d1) in the formula above.
B is incorrect. −0.5411 is −N(d1).
C is incorrect. −0.4589 is N(d1) – 1, which would be the delta of the option if the stock were dividend-free.