
老师好,1、为什么左边是AR(2)?只有Yt和Yt-1,这不是AR(1)吗?
2、为什么AR的形式是(1-L)fai(L)Yt呢?这里的fai(L)是什么意思,之前讲过a(L)=1+a1L+a2L+…,并不是减呢,但是这里是1-0.8L
李坏_品职助教 · 2024年05月09日
嗨,从没放弃的小努力你好:
你在仔细看看我的推导过程,
原版书给出的AR(2)过程(这个是书上举的例子)是:
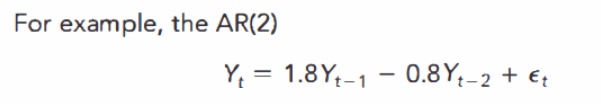
这个移项之后,就是Yt - 1.8Yt-1 + 0.8Yt-2 = 残差,
左边还可以继续变形:
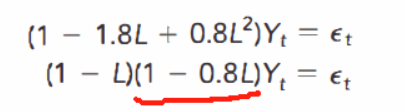
你如果用(1+0.8L),那么左边就无法与Yt - 1.8Yt-1 + 0.8Yt-2相等了。和书上给的AR(2)就不匹配了。
你说的a(L)是p阶滞后多项式,和这里的φ(L)是不一样的,在不同场景下不能混用。
----------------------------------------------
加油吧,让我们一起遇见更好的自己!
梦梦 · 2024年05月10日
也就是a(L)和fai(L)是完全不同的概念
李坏_品职助教 · 2024年05月08日
嗨,从没放弃的小努力你好:
L是lag polynomial,也就是滞后多项式。L可以让任何一个变量得到它的滞后项,L*Yt = Yt-1.
参考原版书:

我们把第一个等式的AR(2)过程改写,也就是右侧只保留残差项,其他的挪到左侧,Yt - 1.8Yt-1 + 0.8Yt-2 = 残差,
而Yt-1 = L*Yt,Yt-2 = L^2 * Yt,
所以Yt - 1.8L*Yt + 0.8L^2*Yt = 残差,所以(1-1.8L + 0.8L^2)*Yt = 残差。
这个等式可以改写为(1-L)*(1-0.8L)*Yt = 残差。
1-0.8L就是讲义里的φ(L),所以(1-L)*φ(L)*Yt = 残差。这就是讲义里的: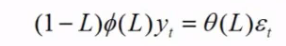
所以可以看到,(1-L)*φ(L)*Yt这种形式,本质上是用到了Yt-1和Yt-2,所以是AR(2)过程。
----------------------------------------------
虽然现在很辛苦,但努力过的感觉真的很好,加油!
梦梦 · 2024年05月09日
老师好,为什么不是(1+0.8L)?a(L)不是等于1+a1L+a2L^2+…apL^p?