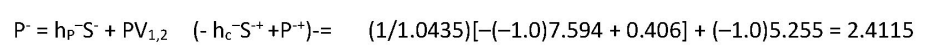NO.PZ2023041003000036
问题如下:
Suppose you observe a non-
dividend- paying Australian equity trading for A$7.35. The call and put options
have two years to mature, the periodically compounded risk- free interest rate
is 4.35%, and the exercise price is A$8.0. Based on an analysis of this equity,
the estimates for the up and down moves are u = 1.445 and d = 0.715,
respectively.
Calculate
the European- style call and put option hedge ratios at Time Step 0 and Time
Step 1. Based on these hedge ratios, interpret the component terms of the
binomial option valuation model.
选项:
解释:
The computation of
the hedge ratios at Time Step 1 and Time Step 0 will require the option values
at Time Step 1 and Time Step 2. The terminal values of the options are given in
Solution 1.
S++ = u2S
= 1.4452(7.35) = 15.347
S+– =
udS = 1.445(0.715)7.35 = 7.594
S– – =
d2S = 0.7152(7.35) = 3.758
S+ = uS
= 1.445(7.35) = 10.621
S– = dS
= 0.715(7.35) = 5.255
Therefore, the
hedge ratios at Time 1 are
In the last hedge
ratio calculation, both put options are in the money (p–+ and p– –). In this
case, the hedge ratio will be –1, subject to a rounding error. We now turn to
interpreting the model’s component terms. Based on the no- arbitrage approach,
we have for the call price, assuming an up move has occurred, at Time Step 1
• C+ = hc+S+ + PV1,2 (- hc+S+- +C+-)-=
0.9476(10.621) + (1/1.0435)[–0.9476(7.594) + 0.0] = 3.1684
Thus, the call
option can be interpreted as a leveraged position in the stock. Specifically,
long 0.9476 shares for a cost of 10.0645 [= 0.9476(10.621)] partially financed
with a 6.8961 {= (1/1.0435)[–0.9476(7.594) + 0.0]} loan. Note that the loan
amount can be found simply as the cost of the position in shares less the
option value [6.8961 = 0.9476(10.621) – 3.1684]. Similarly, we have
• C-= hc–S- + PV1,2 (- h c–S-- +C--)-= 0.0(5.255) + (1/1.0435)[–0.0(3.758) + 0.0] =
0.0
Specifically, long
0.0 shares for a cost of 0.0 [= 0.0(5.255)] with no financing.
For put options,
the interpretation is different. Specifically, we have
P+ =+ hP+S++
+ PV1,2 (- hp+S++
+p++)-=
(1/1.0435)[–(–0.05237)15.347 + 0.0] + (–0.05237)10.621 =
0.2140
Thus, the put
option can be interpreted as lending that is partially financed with a short
position in shares. Specifically, short 0.05237 shares for a cost of 0.55622 [=
(–0.05237)10.621] with financing of 0.77022 {=
(1/1.0435)[–(–0.05237)15.347 + 0.0]}. Note that the lending amount can be
found simply as the proceeds from the short sale of shares plus the option
value [0.77022 = (0.05237)10.621 + 0.2140]. Again, we have
P- = hP–S-
+ PV1,2 (- hc–S-+
+P-+)-=
(1/1.0435)[–(–1.0)7.594 + 0.406] + (–1.0)5.255 = 2.4115
Here, we short 1.0
shares for a cost of 5.255 [= (–1.0)5.255] with financing of 7.6665 {=
(1/1.0435)[–(–1.0)7.594 + 0.406]}. Again, the lending amount can be found
simply as the proceeds from the short sale of shares plus the option value
[7.6665 = (1.0)5.255 + 2.4115].
Finally, The
interpretations remain the same at Time Step 0: c = hcS + PV0,1(–hcS–
+ c–) =
The
interpretations remain the same at Time Step 0:
C=hcS+
PV0,1 (-hcS-+C-)-=
0.5905(7.35) + (1/1.0435)[–0.5905(5.255) + 0.0] = 1.37
Here, we are long
0.5905 shares for a cost of
4.3402 [=0.5905(7.35)] partially financed with
a 2.97 {= (1/1.0435)[–0.5905(5.255) + 0.0] or = 0.5905(7.35) – 1.37} loan.
P = hPS+
PV0,1 (-hPS++P+)=
(1/1.0435){–[–0.4095(10.621)] + 0.214} + (–0.4095)7.35 = 1.36
Here, we short
0.4095 shares for a cost of 3.01 [= (–0.4095)7.35] with financing of 4.37 (=
(1/1.0435){–[–0.4095(10.621)] + 0.214} or = (0.4095)7.35 + 1.36).
这里求p-用的是7.594和0.406(有答案版本文件的37页最上面的公式),这两个数都是p+那个树杈上的,但是根据公式应该是用p-,3.757504和4,242496,为什么要用7.594和0.406?