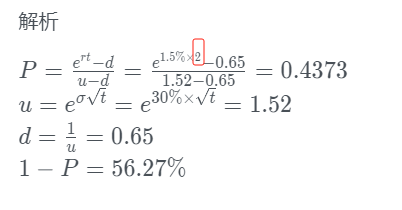NO.PZ2023091802000129
问题如下:
A stock is currently trading at USD 45, and its annual price volatility is 30%. The risk-tree rate is 1.5% per year. A risk manager is developing a 1-step binomial tree for a 2-year horizon. What is the risk-neutral probability that the stock will move down?
选项:
A.
30%
B.
43%
C.
57%
D.
70%
解释:
如题,麻烦说一下用答案这个delta T的原因