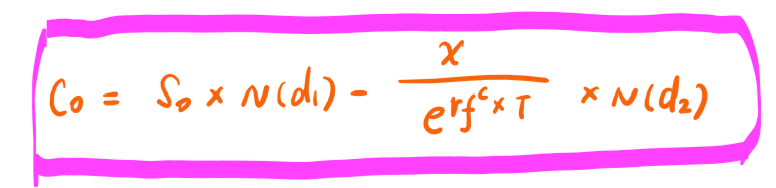问题1:衍生品的线性和非线性是怎么界定的呢?
比如远期Forward是线性衍生品,那表示标的物股价增加1%,远期价值增长是百分之系数(固定值) 即delta?
根据远期定价公式,S0的系数是(1+rf)的T次幂,这应该就是敏感系数,即delta吧。那为什么说远期的delta=1呢?这个东西好像不等于1呀。
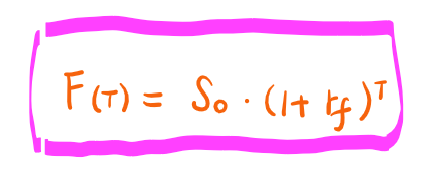
问题2:期权被界定为非线性衍生品,有凸性,涨多跌少。我可以从delta和gamma的图像中理解这个性质。但想问下从BSM公式里,能体现出option的凸性吗?这里面S0的系数即delta就是N(d1),这看起来也是线性的呀,假设N(d1)=0.8,则y=0.8x+常数。它怎么涨多跌少了呢?当股价增加1%,C0增加了0.8%对不对呀?感谢老师~