NO.PZ2023091701000041
问题如下:
A fixed-income portfolio manager currently holds a bullet 7-year US Treasuryp osition with USD 60 million face value.The manager would like to create a cost matching barbell portfolio by purchasing a combination of a 2-year Treasury and a 15-year Treasury that would have the same duration as the7-year US Treasury position.The data for the three US Treasuries are listed below:
Which of the following combinations correctly describes the weights of the
two bonds that the manager will use to construct the barbell portfolio?
选项:
Weightof2-Year Treasury丨Weight of 15-Year Treasury A.14.22%丨85.78%
B.44.46%丨55.54% C.55.54%丨44.46% D.85.78%丨14.22%解释:
To construct a barbell portfolio with the same cost and same duration as the bullet:
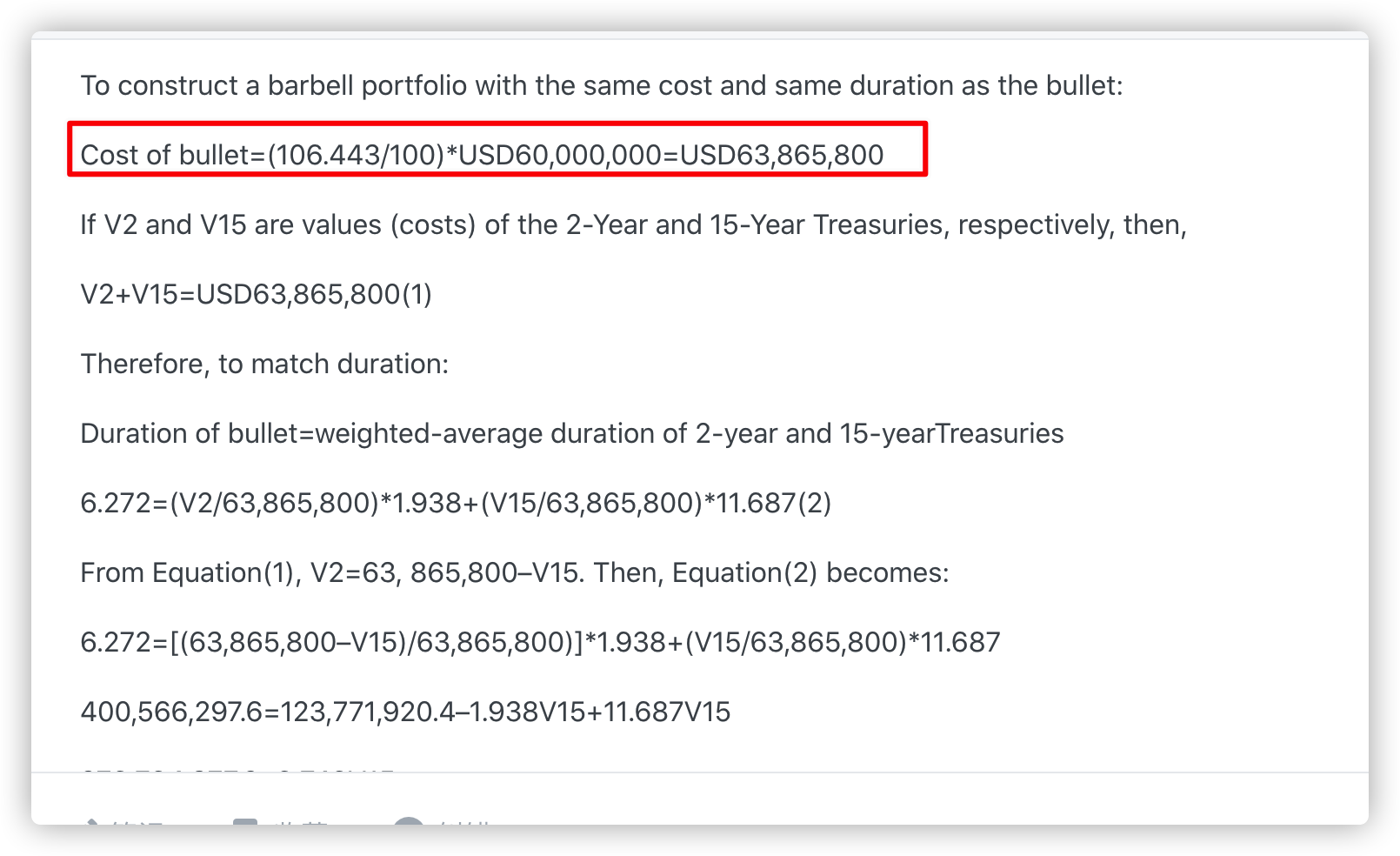
Cost of bullet=(106.443/100)*USD60,000,000=USD63,865,800
If V2 and V15 are values (costs) of the 2-Year and 15-Year Treasuries, respectively, then,
V2+V15=USD63,865,800(1)
Therefore, to match duration:
Duration of bullet=weighted-average duration of 2-year and 15-yearTreasuries
6.272=(V2/63,865,800)*1.938+(V15/63,865,800)*11.687(2)
From Equation(1), V2=63, 865,800–V15. Then, Equation(2) becomes:
6.272=[(63,865,800–V15)/63,865,800)]*1.938+(V15/63,865,800)*11.687
400,566,297.6=123,771,920.4–1.938V15+11.687V15
276,794,377.2=9.749V15
And so,V15=USD28,392,078.90
And so,V2=63,865,800–V15=63,865,800–28,392,078.90=USD35,473,721.10
Giving weight of 2-Year Treasury=35,473,721.10/63,865,800=55.54%
And weight of 15-year Treasury=28,392,078.90/63,865,800=44.46%
A is incorrect. It incorrectly calculates the weights based on duration as: weight of 2-Year T=1.938/(1.938+11.687)=14.22%; and weight of 15-year T=1–0.1422=85.78%.
B is incorrect. It switches the weights derived in C above.
D is incorrect.It switches the weights explained in A above.