00:00 (2X)

李坏_品职助教 · 2024年04月13日
嗨,努力学习的PZer你好:
这两个special case从考试角度来看,只需要掌握最终的两个公式即可,也就是每个case后面的example掌握了就可以应对考题。
正常情况下计算CVA需要用到monte carlo模拟,未来第i期的exposure是不确定的,所以需要通过大量模拟实验,得出平均的exposure, 进而求得第i期由于违约给银行带来的损失现值。
两个special case讲的是一些特殊情况,在这两个特殊情况下,计算CVA不需要进行monte carlo模拟。
特殊情况1:银行与一个对手方签订一份衍生品,这个衍生品只在到期日T为银行带来payoff(例如银行买入一份欧式期权)。因为只有最后到期日这一笔payoff,所以不再需要做模拟实验了,未来的exposure是确定的。主要注意以下几点:
(1)v = f_nd * (1-R),v指的是exposure的现值,而f_nd指的是衍生品现在的no-default value(也就是期权通过BSM模型求出的price),R是recovery rate。
(2)DVA=0, 因为买入期权的时候,只有Long 期权的一方(银行自身)会面临对方的信用风险。所以这份期权考虑了信用风险之后的价值f = f_nd - CVA = f_nd - v * ∑qi,v就是第(1)步里面的,而qi指的是i时刻的违约概率。
(3)前面对期权的分析同样也适用于零息债券,因为零息债券也是只有T时刻一笔payoff. 所以后面一张讲义讲的是用零息债券的价值B和B_nd的比值,等价于期权的价值f和f_nd的比值,可得出f = f_nd * e^-(y-rf)*T。
以上原理能理解最好(重点是最后的公式),考试是以下面的形式出题:
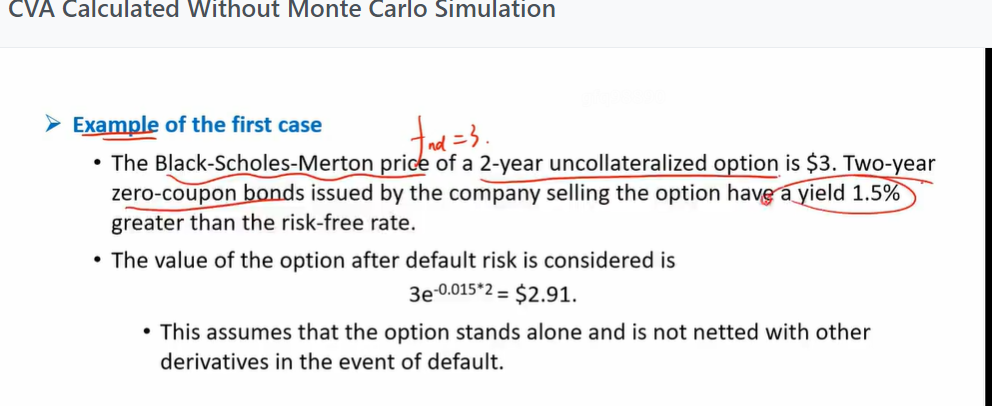
第一个special case掌握这个例题就可以了。也就是计算某个衍生品经过风险调整后的价值f= f_nd * e^-(y-rf)T,这个y-rf就是spread,题目中说的是yield比risk free rate高出1.5%,所以spread就是1.5%,代入公式即可。
再来看特殊情况2:银行与对手方签订远期协议,同意在T时刻按照固定价格K买入某个资产。这份合约在t时刻的exposure也就是远期合约在t时刻的价值与0之间的较大者: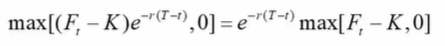 ,这个式子是二者取较大值,求他的数学期望就类似于求期权的价格,所以可以仿照BSM模型对这个exposure求期望,那么t时刻的exposure的数学期望等于:
,这个式子是二者取较大值,求他的数学期望就类似于求期权的价格,所以可以仿照BSM模型对这个exposure求期望,那么t时刻的exposure的数学期望等于:
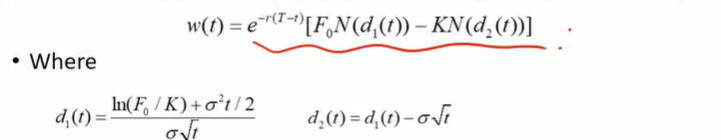
这个公式的w(t)指的就是t时刻的exposure,也就是v.
这个案例也是重点掌握例题:

例题说的是2年期的远期合约,那么我们需要分别算出第一年的exposure的期望v1和第二年的exposure的期望v2。
然后最后要求的是CVA = q1*v1 + q2 * v2,q1和q2题目说分别是2%和3%,v1和v2利用前一张讲义的w(t)公式求解。

同学把这两个example计算过程掌握了就可以了。
----------------------------------------------
就算太阳没有迎着我们而来,我们正在朝着它而去,加油!