NO.PZ2023041003000039
问题如下:
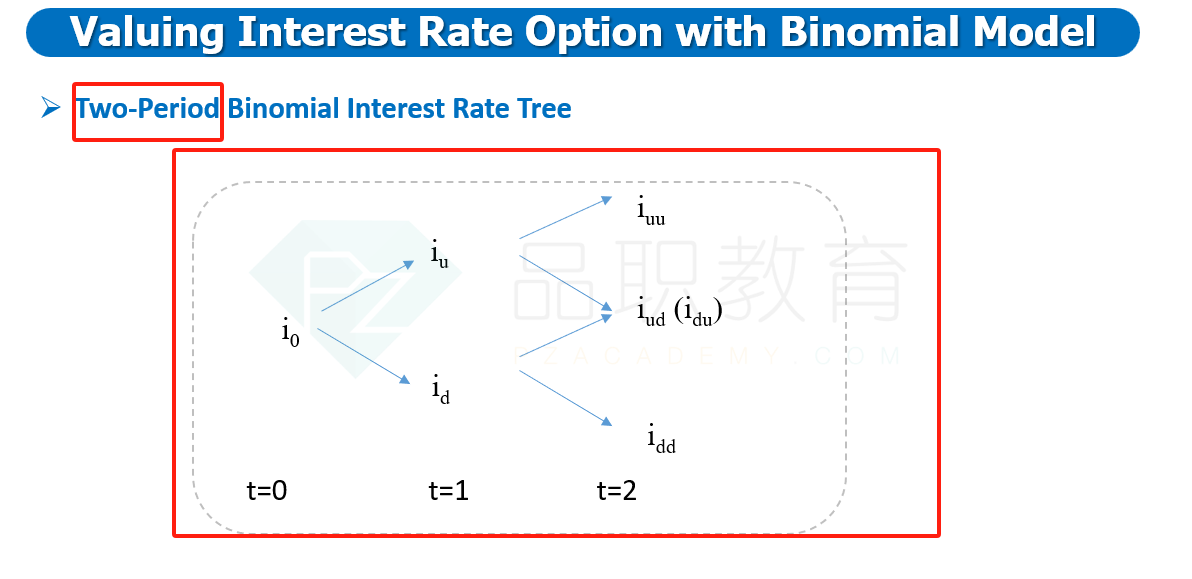
The final option valuation task involves an
interest rate option. Sousa must value a two-year, European-style call option
on a one-year spot rate. The notional value of the option is 1 million, and the
exercise rate is 2.75%. The risk-neutral probability of an up move is 0.50. The
current and expected one-year interest rates are shown in Exhibit 2, along with the values of a one-year
zero-coupon bond of 1 notional value for each interest rate.
Based on Exhibit 2 and the parameters used by
Sousa, the value of the interest rate option is closest to:
选项:
A.5,251.
6,236.
6,429.
解释:
Using the expectations approach, per 1 of
notional value, the values of the call option at Time Step 2 are
c++ = Max(0,5++ - X) =
Max(0,0.050 - 0.0275) = 0.0225.
c+- = Max(0,5+- - X) = Max(0,0.030 - 0.0275) = 0.0025.
c-- = Max(0,5-- - X) =
Max(0,0.010 - 0.0275) = 0.
At Time Step 1, the call values are
c+ = PV[nc++
+ (1 - π)c+-].
c+=
0.961538[0.50(0.0225) + (1 - 0.50)(0.0025)] = 0.012019.
c- = PV[nc+- + (1 - π)c--].
c- = 0.980392[0.50(0.0025) + (1 -
0.50)(0)] = 0.001225.
At Time Step 0, the call option value is
c = PV[πc+ + (1 -
π)c-].
c = 0.970874[0.50(0.012019) + (1 -
0.50)(0.001225)] = 0.006429.
The value of the call option is this amount
multiplied by the notional value, or 0.006429 x 1,000,000 = 6,429.
请问题干说2年,也就是2期的二叉树,为何要用到第三期的节点利率呢?