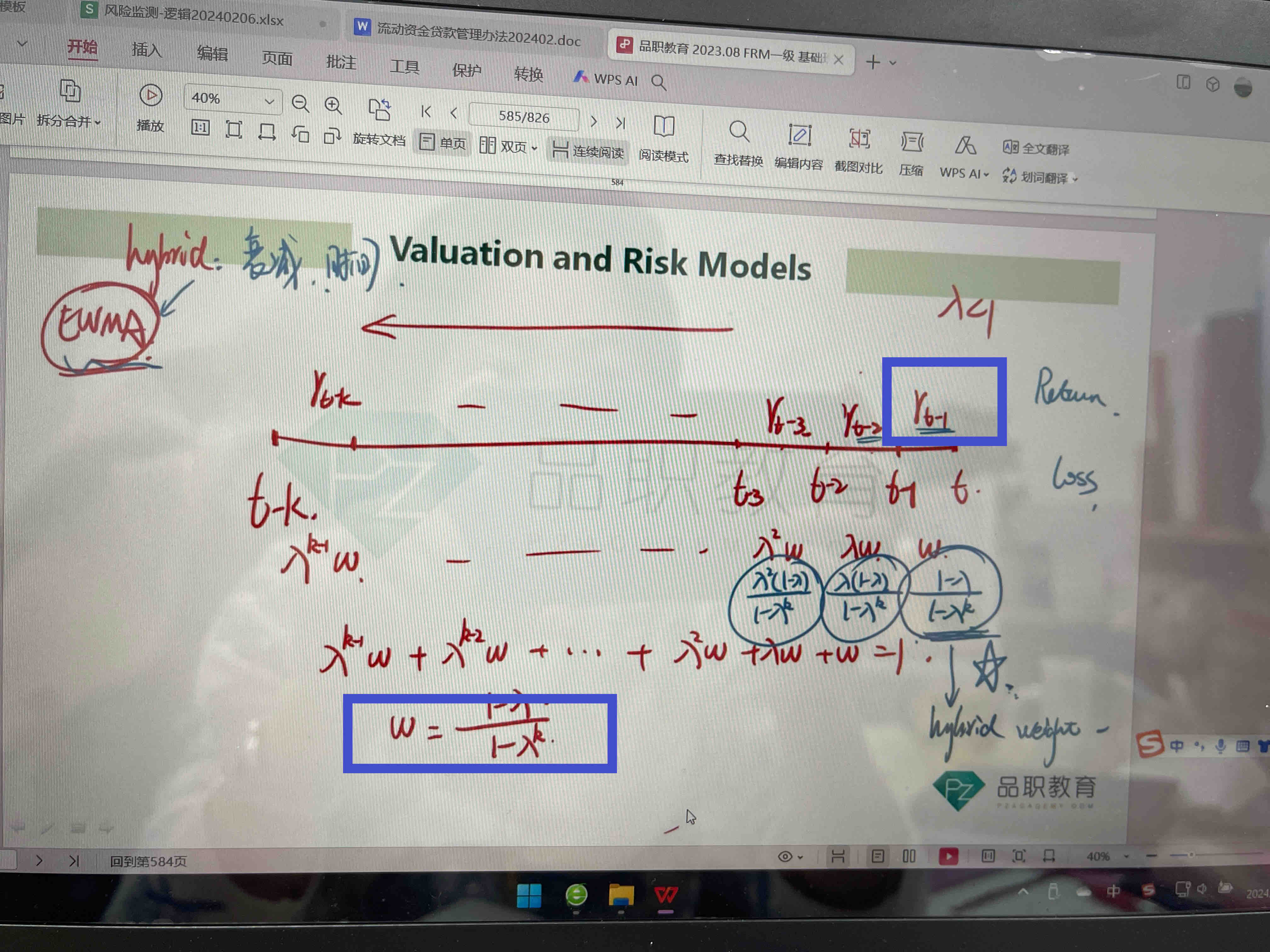
老师您好,这里的时间轴和利率,为什么t-1到t之间的利率是Rt-1呢?为什么不是t-1这一时间点是Rt-1呢?

还有这里的,b大于1,E(x)是发散的,这是什么意思呢?

这里假定Xt是个常数,而不是随机变量,那Xt+1到Xt又是个随机变量,是不确定的?这样合理吗?

这里蓝色的部分不太理解,为什么相当于e的负ht次方?
李坏_品职助教 · 2024年03月11日
嗨,爱思考的PZer你好:
图1里面的w = (1-λ) / (1-λ^k),这个是指数平滑的权重。
首先,把所有R的权重都加起来必须等于1,w + λw + λ^2*w + ... + λ^k-1 * w = 1,等式左边就是w * (1+λ+λ^2 + λ^3 + ... +λ^k-1) = 1,而括号里面是一个等比数列,等比数列求和= 首项*(1-公比^k) / (1-首项),所以:
w * (1+λ+λ^2 + λ^3 + ... +λ^k-1) = w * (1 - λ^k) / (1-λ) = 1,所以w = (1-λ) / (1-λ^k).
2. Xt+1 =a + b* Xt + et+1,这个叫时间序列。当b系数等于1时,是一个随机游走的过程,也就是Xt+1与Xt之间没有关系。如果b小于1,那么X序列是均值回归的,也就是会想着平均值靠近。如果b大于1,那么X序列是发散的,也就是不会靠近X的平均值。
3.图三把括号里的Xt看做常数,是因为当Xt+1 - Xt之后(这也叫一阶差分),剩下的Xt系数非常小了,我们在分析Xt+1 - Xt的方差,可以近似把右边的Xt看做常数。这一行等式的意思是Xt+1 - Xt的方差不是随机的,而是等于σ^2.
4.图四用到了一个高等数学里面求极限的定理: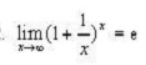
也就是(1+1/x)^x,当x趋近于无穷大时,极限是e。
把1/△t看作x,当△t趋近于0时,x趋近于正无穷。
那么St = (1-h / (1/△t))^(t * 1/△t) = (1 - h*x)^(t * x),这个东西的极限是e^(-t*h)。这个推导过程考试中不会专门考查,这属于大学高等数学的内容了,不是FRM的重点。
----------------------------------------------努力的时光都是限量版,加油!