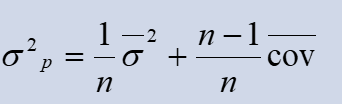NO.PZ2015121801000062
问题如下:
A portfolio manager creates the following portfolio:
If the two securities are uncorrelated, the expected standard deviation of an equal-weighted portfolio is closest to:
选项:
A.14.00%.
B.14.14%.
C.20.00%.
解释:
B is correct.
lσport=w12σ12+w22σ22+2w1w2ρ1,2σ1σ2=(0.5)2(20%)2+(0.5)2(20%)2+2(0.5)(0.5)(0.00)(20%)(20%)=(1.0000%+1.0000%+0.0000%)0.5=(2.0000%)0.5=14.14%
这道题可以用之前讲的多个资产,求方差的公式么?
那个的假设也是没个资产的权重都是一样,刚好和这道题相同
方差的平方=(资产1方差平方+资产2方差平方)/2