如果yield curve 是upward sloping, 可以得出f(2,1)大于f(1,2)的结论吗? 我记得何老师在课上说两者的时间点是不同的,所以都不在一条curve上,所以是不能比较的。
但是今天群里有小伙伴推出来 f(2,1) 大于f(1,2), 我总觉得哪里不对。
发亮_品职助教 · 2018年06月06日
不一定的!
这主要取决于收益率曲线的陡峭程度。
我是将forward rate理解成:将某个spot rate,延长至另一个spot rate的marginal rate;
终点一样,起点不一样的话,marginal rate的大小不一定谁大谁小,要看曲线的陡峭的变化程度。
说起来感觉有点乱,我举一个数据例子,这个是upward-sloping的:
1-year spot rate = 5%
2-year spot rate = 9.8%
3-year spot rate = 10%
我们可以计算f(2,1)

也可以计算f(1,2)
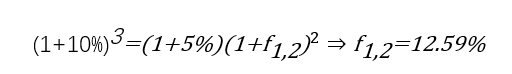
发现f(1,2)是大于f(2,1)的。
但是如果我把数据换一下,同样是upward-sloping,f(2,1)又是大于f(1,2):
比如,1-year spot rate = 2%,;2-year spot rate =3%;3-year是10%;
这个一定是f(2,1)大于f(1,2)的;
这就是收益率曲线的陡峭程度不一样。
我们考试只要会判断forward与spot之间的关系就好了。