拿current举例,就是
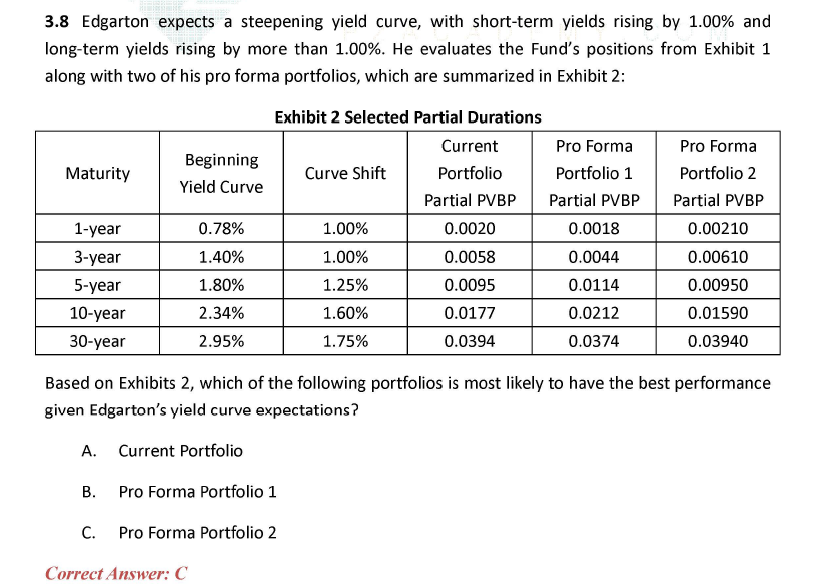
delta = - (0.0020*1 + 0.0058*1 + 0.0095*1.25 + 0.0177*1.6 + 0.0394*1.75) = -0.1169
Portfolio 1 和 2 的变化数值分别是 - 0.1198 和 -0.1144,因为yield curve 总体上移,所以 portfolio 2下降最少,performance最好。
不知道我这个算法有没有道理?
lemorning · 2018年05月30日

拿current举例,就是
delta = - (0.0020*1 + 0.0058*1 + 0.0095*1.25 + 0.0177*1.6 + 0.0394*1.75) = -0.1169
Portfolio 1 和 2 的变化数值分别是 - 0.1198 和 -0.1144,因为yield curve 总体上移,所以 portfolio 2下降最少,performance最好。
不知道我这个算法有没有道理?
发亮_品职助教 · 2018年06月01日
粗略的比较,不能保证一定会最优。要算一下。
假设单纯看30年portfolio2表现更差,看10-,5-year时,portfolio2表现更好,如果表现好的部分小于表现差的部分,综合看30-,10-,5-year,portfolio2仍然不如portfolio1好。
也就是说,即便5-year,10-year portfolio2表现更好,但是不足以弥补30年表现差的部分。那么综合这三个期限来看,portfolio2仍然是表现更差的。
本题的实际情况是30年portfolio2表现更差,但是并没有差多少;在10年期,portfolio2表现更好,不但弥补了30年表现差的部分,还有余额,使得portfolio2表现优于了portfolio1。5-year,portfolio2表现更好,进一步使得portfolio2在综合比较,5-,10-,30-year时,表现更好。(以上是通过计算了收益率变动对债券价格的影响后比较的)。
同理,最好还要算一下1-year,3-year对债券价格的影响。
所以本题最好按你最开始用的方法计算一下,最保险!
发亮_品职助教 · 2018年05月31日
这么算完全没有问题!
不过在乘以partial PVBP时,用到的收益率曲线变动单位应该是bp,而不是1%;但是这道题不考虑单位也没问题,因为大家单位都一样,相当于同时放大了100倍。
PVBP衡量的是收益率曲线变动1bp时(平行移动、收益率曲线整体移动),债券的价格变动多少元。
而Partial PVBP衡量收益率曲线在其他maturity的收益率保持不变的情况下,仅仅某年的收益率发生改变1bp,债券价格变动多少元。如本题,1-year partial PVBP的0.0020表示为:3-year, 5-year, 10-year, 30-year的收益率不变,仅仅是1-year的收益率变动1bp,那么整个bond portfolio的价值变动0.0020。
这么看的话,partial PVBP加总应该等于PVBP。
既然题目给出了每一个maturity的收益率变动幅度,也给出了每一个partial PVBP,把他们相乘加总,得到的就是债券portfolio价格变动都少钱。
所以你这么算完全没有问题。可以做对题。
但是你的解释有一些问题。另外,portfolio 2表现更好,是受到两个因素的综合影响,第一是duration,第二是key rate duration的分布。
另外要注意的是,这道题的收益率曲线的变动,是包含两个变动的:
所以收益率曲线的变动是:平行向上移动 + steepening。
所以要判断哪个portfolio表现的更好,第一要看portfolio总的duration的影响,在本题中,由于收益率曲线整体上升1%,所以可以算出duration平行移动时的价格变动。
第二,由于收益率曲线还包括steepening,在本题中,还要比较5-year,10-year,30-year,这三个steepening点位,哪个portfolio的key rate duration更小。这样受到额外steepening的影响较小。所以要算Key rate duration对债券portfolio价格的影响。
两者综合起来才是这道题收益率变动对债券portfolio价格的影响。
lemorning · 2018年05月31日
谢谢助教的解答。另一个问题是,如果用直接比较partial PVBP的方法话,portfolio 2 在30年期受影响大于portolio1,其他 5Y 10Y 小于Portfolio1. 整体看的话,一定是 Portfolio 2受影响最小吗,表现最优吗?