问题如下图:

选项:
A. 
B.  不太明白PV_和PV+是如何计算出的?可以写得具体些吗?谢谢
不太明白PV_和PV+是如何计算出的?可以写得具体些吗?谢谢
C. 
解释:

发亮_品职助教 · 2018年05月30日
先算利率整体下移30bps的情形,算出来就是PV-。
上移的做法一样,建议一定自己求一下上移的情形,二叉树是重点,一定要掌握!
利率整体下移30bps有以下二叉树:
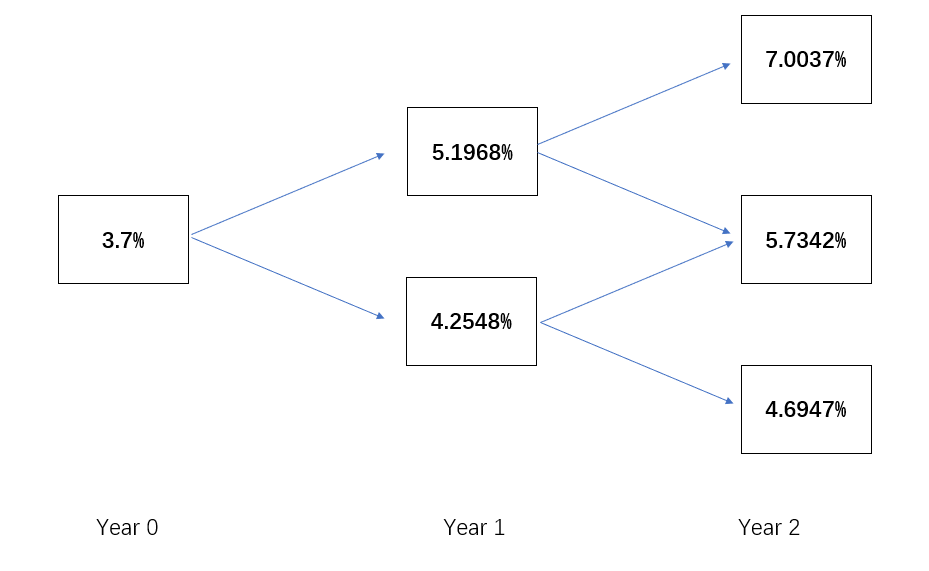
注意这是benchmark的二叉树,AI这只债券有OAS:13.95bps,所以要加上OAS算出来AI这只债券的二叉树:

债券第三年到期,将第三年的面值加上coupon折现到第二年末各个节点;用到的是第二年末开始的one-year forward rate。
如下图,所以V2.UU = 98.23;V2.UL = 99.41;V2.LL=100.39。
只有V2.LL折现后的价值大于行权价,所以将这个节点的债券价格调整到行权价100.
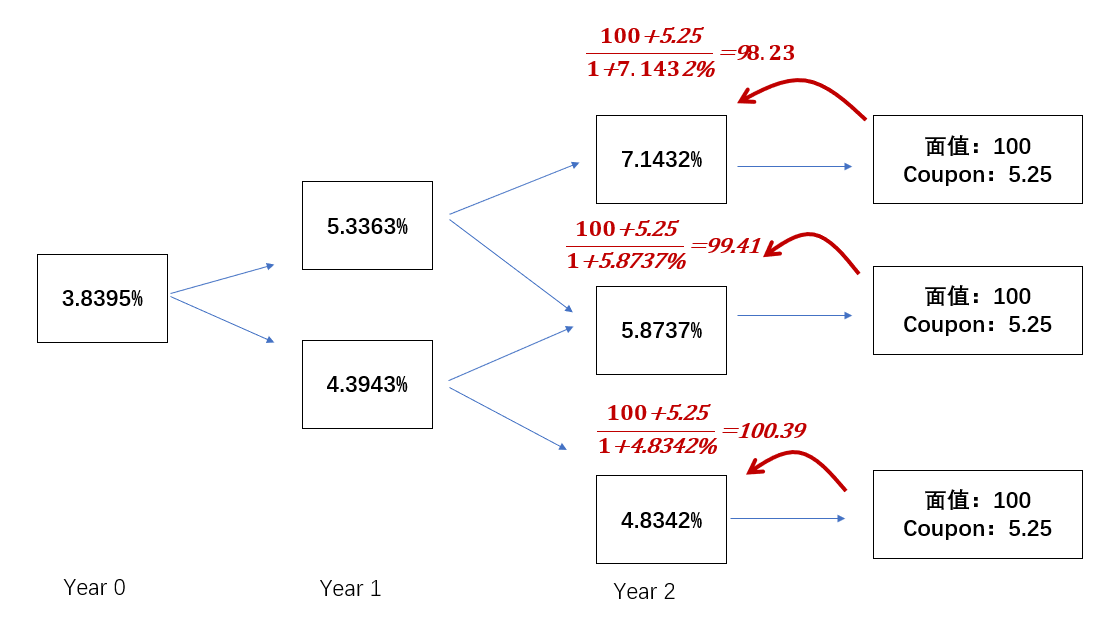
所以我们得到V2.UU = 98.23;V2.UL = 99.41;V2.LL=100
然后再将第二年年末各个节点的债券价值加上Coupon折现到 V1.U和V1.L;
先看V1.U:
由于从V1.U开始会有两个树杈,V2.UU,及V2.UL,各自的情况是50%,都折现到V1.U,取加权平均后就是V1,U的债券价值,先将V2.UU,V2.UL折现到V1.U,如下图:

取加权平均,所以V1.U的债券价值为:

再看V1.L;
由于从V1.L开始会有两个树杈,V2.LL,及V2.UL,各自的情况是50%,各自折现到V1.L,然后加权平均就是V1,L的债券价值,先将V2.LL,V2.UL折现到V1.L,如下图:

求加权平均就是V1.L的价值:
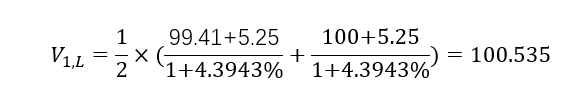
发现V1.L的价值大于行权价,所以触发行权,将债券价格调整到行权价100
所以有:V1.U=98.795;有V1.L=100
最后再将year1各节点调整后的价格折现到现在时刻,从现在时刻,往第一年发展会有2个分叉,V1.U,V1.L,两个分叉各50%,所以折现加权后是可以求出债券现在时刻的价格:


总结一下:
daiqiedison · 2018年06月22日
这题也太夸张了,虽然知道这么算,但是算出来半个小时没有了。
发亮_品职助教 · 2018年06月22日
这个能是二叉树里,能考的最复杂的,主要是算的多,其实也没啥技术含量,就是要细心。
NO.PZ201712110200000401 问题如下 Baseon Exhibits 1 an2, the effective ration for the bonis closest to: A.1.98. B.2.15. C.2.73. B is correct. The bons value if interest rates shift wn 30 bps (PV–) is 100.78. The bons value if interest rates shift up 30 bps (PV+) is 99.487.Effective ration=[(PV-)-(PV+)]/[2× (ΔCurve) × (PV0)]= (100.780 - 99.487)/ (2 × 0.003 × 100.200)=2.15 bons value if interest rates shift wn 30 bps (PV–) 我算的不是 100.78,而是101.03854,算了两次都是这样,请问我哪里出错了?
NO.PZ201712110200000401 问题如下 Baseon Exhibits 1 an2, the effective ration for the bonis closest to: A.1.98. B.2.15. C.2.73. B is correct. The bons value if interest rates shift wn 30 bps (PV–) is 100.78. The bons value if interest rates shift up 30 bps (PV+) is 99.487.Effective ration=[(PV-)-(PV+)]/[2× (ΔCurve) × (PV0)]= (100.780 - 99.487)/ (2 × 0.003 × 100.200)=2.15 老师您好,我看原教材解析里面都懒得写计算全过程了...... 一般考试中会出现这么繁琐的计算么
NO.PZ201712110200000401问题如下Baseon Exhibits 1 an2, the effective ration for the bonis closest to:A.1.98.B.2.15.C.2.73.B is correct. The bons value if interest rates shift wn 30 bps (PV–) is 100.78. The bons value if interest rates shift up 30 bps (PV+) is 99.487.Effective ration=[(PV-)-(PV+)]/[2× (ΔCurve) × (PV0)]= (100.780 - 99.487)/ (2 × 0.003 × 100.200)=2.15对于含权债券如何判断题目给的现金流是否含权,什么时候需要在分母加oas
NO.PZ201712110200000401 问题如下 Baseon Exhibits 1 an2, the effective ration for the bonis closest to: A.1.98. B.2.15. C.2.73. B is correct. The bons value if interest rates shift wn 30 bps (PV–) is 100.78. The bons value if interest rates shift up 30 bps (PV+) is 99.487.Effective ration=[(PV-)-(PV+)]/[2× (ΔCurve) × (PV0)]= (100.780 - 99.487)/ (2 × 0.003 × 100.200)=2.15 老师上课说过,OAS是剔除了权利影响的sprea分子的现金流已经包含了权利影响了。那为什么还可以在二叉树的利率上直接加OAS,但是现金流又还是按照初始的coupon rate来计算呢?
NO.PZ201712110200000401 问题如下 Baseon Exhibits 1 an2, the effective ration for the bonis closest to: A.1.98. B.2.15. C.2.73. B is correct. The bons value if interest rates shift wn 30 bps (PV–) is 100.78. The bons value if interest rates shift up 30 bps (PV+) is 99.487.Effective ration=[(PV-)-(PV+)]/[2× (ΔCurve) × (PV0)]= (100.780 - 99.487)/ (2 × 0.003 × 100.200)=2.15 例如上图是辅导老师的解题过程,V+在year2,既然折现率4.9377%小于coupon rate,作为callable,为什么不直接取100呢而是99.7114?