NO.PZ201702190300000306
问题如下:
The value of the American-style put option on Beta Company shares is closest to:
选项:
A.4.53.
B.5.15.
C.9.32.
解释:
B is correct.
Using the expectations approach, the risk-neutral probability of an up move is
π= [FV(1) - d]/(u - d) = (1.03 - 0.800)/(1.300 - 0.800) = 0.46.
An American-style put can be exercised early. At Time Step 1, for the up move, p+ is 0.2517 and the put is out of the money and should not be exercised early (X < S, 40 < 49.4). However, at Time Step 1, p- is 8.4350 and the put is in the money by 9.60 (X - S = 40 - 30.40). So, the put is exercised early, and the value of early exercise (9.60) replaces the value of not exercising early (8.4350) in the binomial tree. The value of the put at Time Step 0 is now
p = PV[πp+ + (1 - π)p-] = [1/(1.03)][0.46(0.2517) + 0.54(8.4350)] = 4.54.
Following is a supplementary note regarding Exhibit 1.
The values in Exhibit 1 are calculated as follows.
At Time Step 2:
p++ = Max(0,X - u2S) = Max[0,40 - 1.3002(38)] = Max(0,40 - 64.22) = 0.
p-+ = Max(0,X - udS) = Max[0,40 - 1.300(0.800)(38)] = Max(0,40 - 39.52) = 0.48.
p- - = Max(0,X - d2S) = Max[0,40 - 0.8002(38)] = Max(0,40 - 24.32)= 15.68.
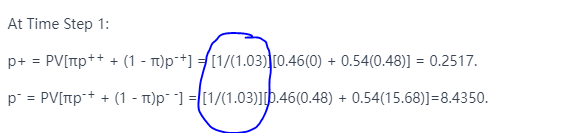
At Time Step 1:
p+ = PV[πp++ + (1 - π)p-+] = [1/(1.03)][0.46(0) + 0.54(0.48)] = 0.2517.
p- = PV[πp-+ + (1 - π)p- -] = [1/(1.03)][0.46(0.48) + 0.54(15.68)]=8.4350.
At Time Step 0:
p = PV[πp+ + (1 - π)p-] = [1/(1.03)][0.46(0.2517) + 0.54(9.6)] = 5.1454.
中文解析:
本题考察的是计算美式看跌期权的价值,需要注意的是在t=1的节点,需要判断是否有必要提前行权。
在本题中,在p- 的确定时,就需要考虑这个问题,如果在t=1时刻立即行权,p- 等于9.6,如果在t=2时刻行权,折现后求得的p- 为8.4350.两者取大,因此应该在t=1时刻行权,得到p- 等于9.6.
然后再根据p- =9.6,p+ =0.2517折现到0时刻得到p0.

P+和P-为什么不统一呢,就是折现就都折现,不折现就都不折现,怎么有的折现有的是直接算的?