开发者:上海品职教育科技有限公司 隐私政策详情

应用版本:4.2.11(IOS)｜3.2.5(安卓)APP下载

返回

𝒜𝒩𝒥𝒜 安雅🎃 · 2023年07月25日

请讲讲解题思路（题目把duration和VaR结合起来）

  1. FRM I
  2. Valuation And Risk Models

NO.PZ2016082402000054

问题如下：

A portfolio consists of two zero-coupon bonds, each with a current value of $10. The first bond has a modified duration of one year and the second has a modified duration of nine years. The yield curve is flat, and all yields are 5%. Assume all moves of the yield curve are parallel shifts. Given that the daily volatility of the yield is 1%, which of the following is the best estimate of the portfolio’s daily value at risk (VAR) at the 95% confidence level?

选项：

A.

USD 1.65

B.

USD 2.33

C.

USD 1.16

D.

USD 0.82

解释：

ANSWER: A

The dollar duration of the portfolio is 1×$10+9×$10=$100\times\$10+9\times\$10=\$100 . Multiplied by 0.01 and 1.65, this gives $1.65.

一个组合包含两个零息债券，每一个债券价格10，第一个债券的MD=1，第二个MD=9，利率全部是5%。假设利率都是平行移动，每日的波动率为1%，请问95%置信区间下的dailyVaR是多少？

％VAR＝σ*Z(0.95)=1%*1.65

95%时z=1.65

组合的Dollar Duration=1*10+9*10=100

VaR=100*1.65*1%=1.65

助教你好：


这题把duration和VaR结合起来之后让我不知从何下手。


我首先想到dollar VaR这个式子，z=1.65，sigma=0.01，asset value=20，可是这样算的话就没答案。


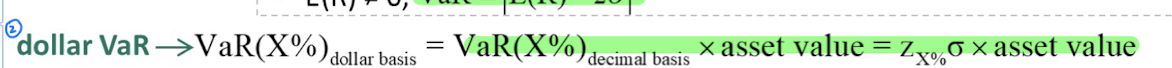
题干给出了两只债券各自的duration，要怎么用上这个条件？


我还看见这同学问到了讲义上没有的dollar duration： https://class.pzacademy.com/qa/97506。


所以我想了解，拿到这道题之后，我首先该往哪个方向去思考？谢谢。


添加评论
1 个答案

李坏_品职助教 · 2023年07月25日

嗨，爱思考的PZer你好：


题目最后问的是VaR，传统的daily VaR计算公式是: VaR=value * |μ-Z*σ|，Z是1.65，σ是1%，μ是收益率，题目没说，可以默认为是0.


注意题目给的1%这个条件是“volatility of the yield is 1%”，也就是债券的到期收益率的波动率为1%，到期收益率的波动率是通过duration进而影响资产价值变动的，所以公式最前面的value要改为duration * value，也就是dollar duration，是100.


你说的用asset value直接乘以Z和σ，那个σ是资产的波动率，而不是到期收益率的波动率。


----------------------------------------------
加油吧，让我们一起遇见更好的自己！

  • 1

    回答

  • 1

    关注

  • 407

    浏览
相关问题

NO.PZ2016082402000054问题如下 A portfolio consists of two zero-coupon bon, eawith a current value of $10. The first bonha mofieration of one yeanthe seconha mofieration of nine years. The yielcurve is flat, anall yiel are 5%. Assume all moves of the yielcurve are parallel shifts. Given ththe ily volatility of the yielis 1%, whiof the following is the best estimate of the portfolio’s ily value risk (VAR) the 95% confinlevel? US1.65 US2.33 US1.16 US0.82 ANSWER: AThe llration of the portfolio is 1×$10+9×$10=$100\times\$10+9\times\$10=\$100×$10+9×$10=$100 . Multiplie0.01 an1.65, this gives $1.65.一个组合包含两个零息债券，每一个债券价格10，第一个债券的M1，第二个M9，利率全部是5%。假设利率都是平行移动，每日的波动率为1%，请问95%置信区间下的ilyVaR是多少？％VAR＝σ*Z(0.95)=1%*1.6595%时z=1.65组合的llration=1*10+9*10=100VaR=100*1.65*1%=1.65 老师，为什么要乘以llvalue，而不是乘以各自的value10？

2023-04-28 11:58 2 · 回答

NO.PZ2016082402000054问题如下 A portfolio consists of two zero-coupon bon, eawith a current value of $10. The first bonha mofieration of one yeanthe seconha mofieration of nine years. The yielcurve is flat, anall yiel are 5%. Assume all moves of the yielcurve are parallel shifts. Given ththe ily volatility of the yielis 1%, whiof the following is the best estimate of the portfolio’s ily value risk (VAR) the 95% confinlevel? US1.65 US2.33 US1.16 US0.82 ANSWER: AThe llration of the portfolio is 1×$10+9×$10=$100\times\$10+9\times\$10=\$100×$10+9×$10=$100 . Multiplie0.01 an1.65, this gives $1.65.一个组合包含两个零息债券，每一个债券价格10，第一个债券的M1，第二个M9，利率全部是5%。假设利率都是平行移动，每日的波动率为1%，请问95%置信区间下的ilyVaR是多少？％VAR＝σ*Z(0.95)=1%*1.6595%时z=1.65组合的llration=1*10+9*10=100VaR=100*1.65*1%=1.65 ​平均ration是（1*10+9*10）/20=5 请问这个是在讲义的哪一页有讲到？完全不记得了。。。

2023-04-27 16:09 1 · 回答

NO.PZ2016082402000054问题如下 A portfolio consists of two zero-coupon bon, eawith a current value of $10. The first bonha mofieration of one yeanthe seconha mofieration of nine years. The yielcurve is flat, anall yiel are 5%. Assume all moves of the yielcurve are parallel shifts. Given ththe ily volatility of the yielis 1%, whiof the following is the best estimate of the portfolio’s ily value risk (VAR) the 95% confinlevel? US1.65 US2.33 US1.16 US0.82 ANSWER: AThe llration of the portfolio is 1×$10+9×$10=$100\times\$10+9\times\$10=\$100×$10+9×$10=$100 . Multiplie0.01 an1.65, this gives $1.65.一个组合包含两个零息债券，每一个债券价格10，第一个债券的M1，第二个M9，利率全部是5%。假设利率都是平行移动，每日的波动率为1%，请问95%置信区间下的ilyVaR是多少？％VAR＝σ*Z(0.95)=1%*1.6595%时z=1.65组合的llration=1*10+9*10=100VaR=100*1.65*1%=1.65 一直想问这个平行移动涉及的计算在基础课哪一部分

2023-04-27 15:44 1 · 回答

NO.PZ2016082402000054问题如下 A portfolio consists of two zero-coupon bon, eawith a current value of $10. The first bonha mofieration of one yeanthe seconha mofieration of nine years. The yielcurve is flat, anall yiel are 5%. Assume all moves of the yielcurve are parallel shifts. Given ththe ily volatility of the yielis 1%, whiof the following is the best estimate of the portfolio’s ily value risk (VAR) the 95% confinlevel? US1.65 US2.33 US1.16 US0.82 ANSWER: AThe llration of the portfolio is 1×$10+9×$10=$100\times\$10+9\times\$10=\$100×$10+9×$10=$100 . Multiplie0.01 an1.65, this gives $1.65.讲义中提到的都是ration和01，一个是%的概念，一个是llar的概念，但是没有提到过llration，所以llration就是ration*market value？

2022-04-05 17:43 1 · 回答