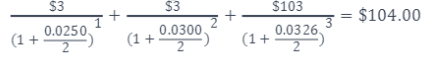NO.PZ2019070101000037
问题如下:

Based on the table, the value of a 1.5-year, 6% semiannual coupon, $100 par value bond is closest to:
选项:
A.$102.19.
B.$103.42.
C.$104.00.
D.$105.66.
解释:
C is correct
考点:Bond Price
解析:
请根据图表信息求出期限1.5年,半年付息一次,coupon rate为6%,面值为100的债券价格。
债券价格等于债券未来现金流的折现求和,每一笔coupon的折现率应使用对应期限的spot rate。Bond price =
讲义上一道类似的题何老师给出了三种方法,折现因子、spot rate和forward rate来做。请问这道题可以用折现因子解答吗