NO.PZ2020011303000048
问题如下:
An investment has probabilities of 0.1, 0.3, 0.2, 0.3, and 0.1 of giving one-year returns equal of 30%, 20%, 10%, 0%, and −10%. What is the mean return and the standard deviation of the return?
解释:
The mean return is 10%. The expected squared return is 0.024 so that the standard deviation of
有一个投资产品获得30%回报率的可能性是0.1,20%回报率的可能性是0.3,10%回报率的可能性是0.2,0%回报率的可能性是0.3,-10%回报率的可能性是0.1。
求回报率的均值与标准差
均值=0.1*30%+0.3*20%+0.2*10%+0.3* 0%+0.1*(-10%)=0.1=10%
expected squared return=0.1*(30%)^2+0.3*(20%)^2+0.2*(10%)^2+0.3*(0%)^2+0.1*(-10%)^2=0.024
标准差=(0.024-01*0.1)^(1/2)=0.118 or 11.8%.
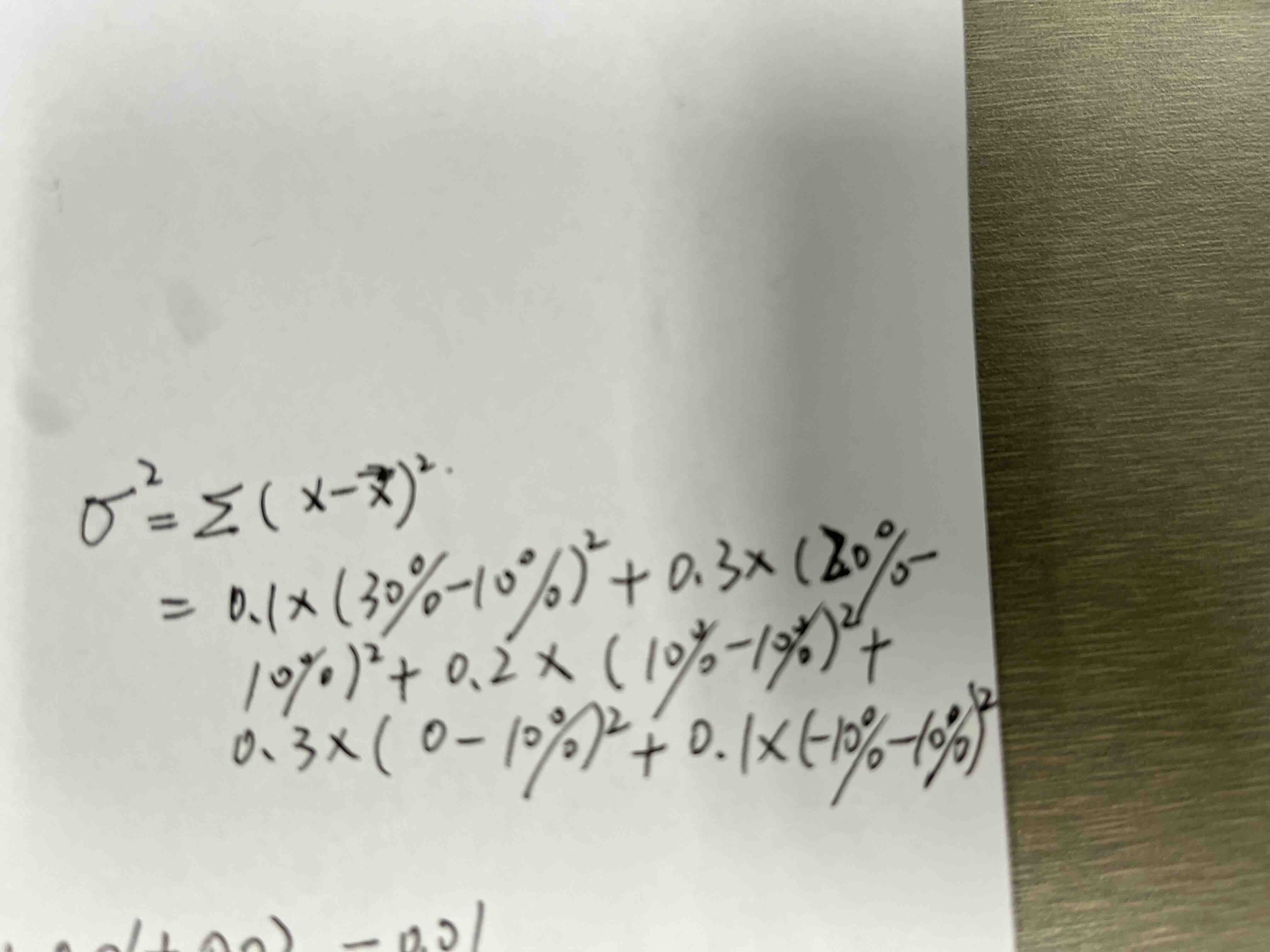
是这么计算可以吗?另外用计算器该怎么算



