为何这句话是对的？

嗨，从没放弃的小努力你好：

我的意思就是delta-normal算出的var更大。delta-normal算出来的跌的更多，所以用它算是高估了。

所以开头你问的这个“A delta normal method will understate the risk of an options portfolio.”这句话我觉得是错的。

----------------------------------------------
虽然现在很辛苦，但努力过的感觉真的很好，加油！

嗨，爱思考的PZer你好：

首先这个考点只需要知道结论即可，不会考你数学推导。

这个公式和这段话是原版书教材里面的，可以看一下FRM原版书。

教材里还给了一张图，图里面的虚线（45度直线）是delta-normal的期权价格，而实线则是实际上的期权价格。可以看到实际的期权价格比45度的虚线要多了一些弧度，也就是curvature，这个弧度的效果就是，对于一定比例的股票价格变动（横坐标变动），实际的期权价格的上涨，会比45度的虚线要多，所以△P=δ*△S + 1/2 * γ * △S^2。

这里的△P是期权价格的变化，△P后面是泰勒展开（高数里面那个泰勒展开），一般只考虑前两项，也就是一次项和二次项就足够了。

如果只考虑一次项，那就是delta normal method，这样就忽略了后面大于零的二次项，所以是低估了期权的价格。比如本来最极端的5%的概率下，期权的价格应该是只下跌30%，但由于忽略了二次项，导致5%的概率的期权价格跌了35%，这就说明delta-normal的α=5%的VaR被夸大了。

----------------------------------------------
加油吧，让我们一起遇见更好的自己！

嗨，从没放弃的小努力你好：

你在哪里看到的这句话？delta-normal是忽略了期权的二次项变动的，

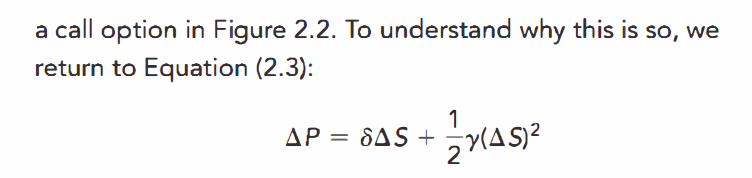
也就是上面公式的γ=0了，会使得期权价格变动被低估，从而使得VaR的值被夸大了。应该是高估了风险。

按照FRM原版书的原文讲解：

----------------------------------------------
加油吧，让我们一起遇见更好的自己！