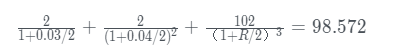NO.PZ2020021204000012
问题如下:
The six-month and one-year zero rates are 3% and 4% (both compounded semi-annually) and a 1.5-year bond paying a coupon of 4% per annum semi-annually has a yield of 5%. What is the 1.5-year zero-coupon interest rate?
解释:
The price of the 1.5-year bond with a face value of 100 is:
If the 1.5-year zero rate is R we must have:
The solution to this equation is R = 0.05027. The 1.5-year zero rate is therefore 5.027%.
麻烦介绍下该类题型怎么做?谢谢