NO.PZ2020010301000005
问题如下:
Based on the probabilities in the plot below, what are the values of the following?
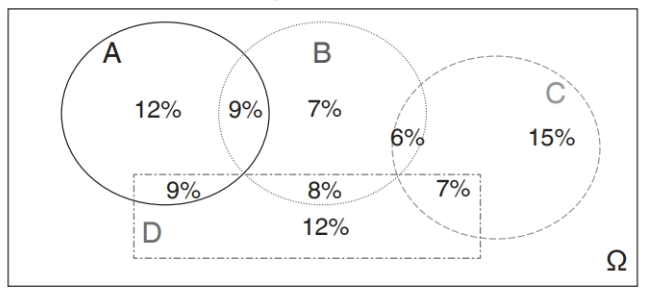
a.
b. Pr(D|A∪B∪C)
c. Pr(A|A)
d. Pr(B|A)
e. Pr(C|A)
f. Pr(D|A)
g.
h.
i. Are any of the four events pairwise independent?
选项:
解释:
a. 1 - Pr(A) = 100% - 30% = 70%
b. This value is Pr(D∩(A∪B∪C))/Pr(A∪B∪C). The total probability in the three areas A, B, and C is 73%. The overlap of D with these three is 9% + 8% + 7% = 24%, and so the conditional probability is 24%/73%= 33%.
c. This is trivially 100%.
d. Pr(B∩A) = 9%. The conditional probability is 9%/30% = 30%.
e. There is no overlap and so Pr(C∩A) = 0.
f. Pr(D∩A) = 9%. The conditional probability is 30%.
g. This is the total probability not in A or D. It is 1 – Pr(A∪D) = 1 - (Pr(A) + Pr(D) - Pr(A∩D)) = 100% - (30% + 36% - 9%) = 43%.
h. This area is the intersection of the space not in A with the space not in D. This area is the same as the area that is not in A or D, and so 43%.
i. The four regions have probabilities A = 30%, B = 30%, C = 28% and D = 36%. The only region that satisfied the requirement that the joint probability is the product of the individual probabilities is A and B because Pr(A∩B) = 9% = Pr(A)Pr(B) = 30% * 30%.
a. 的式子表示的是什么意思,包括后面的字母上方有C的次方



