NO.PZ2020021205000042
问题如下:
What is the vega of a European put option on a stock index when the index level is USD 1,500, the strike price is USD 1,400, the risk-free rate is 5%, the dividend yield is 2%, the volatility is 18%, and the time to maturity is three months. How can this be interpreted?
选项:
解释:
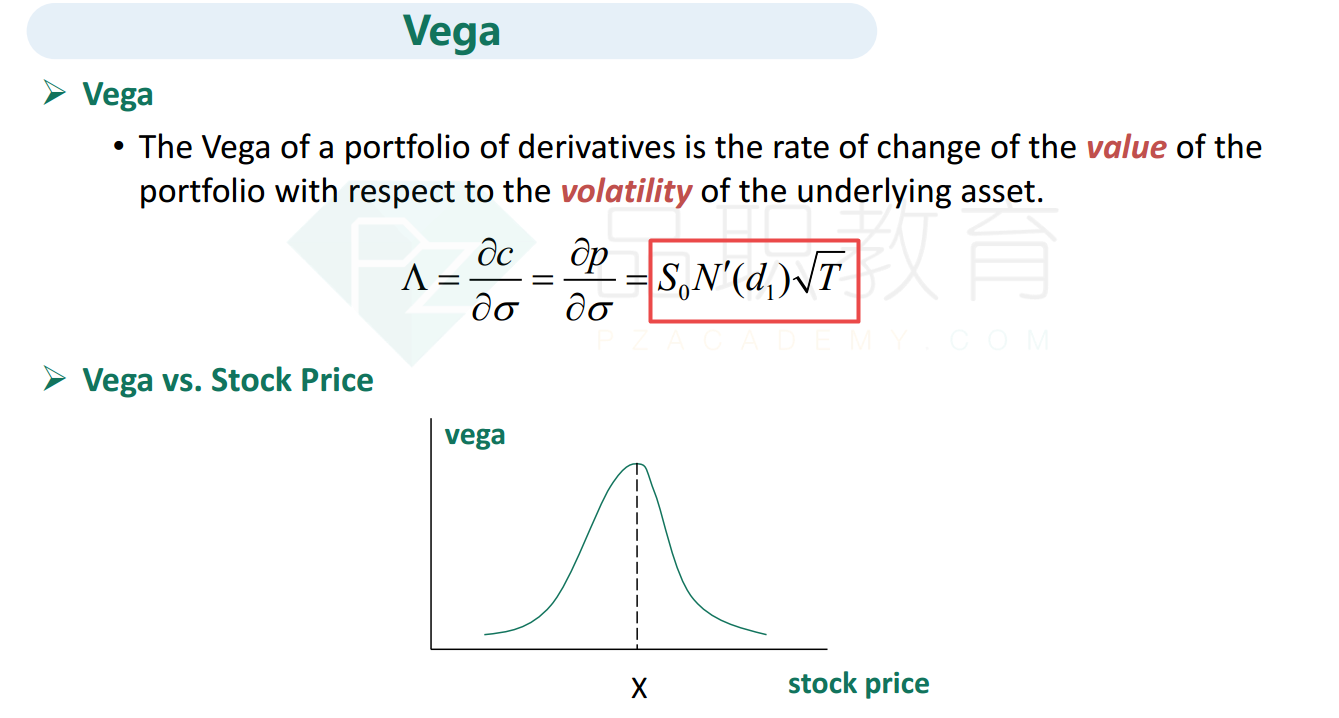
The vega is SoN'(d1 )
In this case, S0 = 1,500, K = 1,400, r = 0.05, q = 0.02, = 0.18, and T = 0.25.
d1== 0.8949
and vega is
1 500 X *=199
This means that the value of a long position increases by 199 X 0.01 = 1.99 if volatility increases by 1% (= 0.01) from 18% to 19%. Similarly, it decreases by 1. 99 if the volatility decreases from 18% to 17%.
老师,VEGA的计算公式是什么?在基础讲义哪页?答案中公式和后面带的数据好像不一致。考纲要求Vega计算吗?谢谢