
老师您好,能否推导一下期望properties的序号2和序号5呢?谢谢🙏
pzqa27 · 2023年02月13日
嗨,努力学习的PZer你好:
额,同学如果看不懂连加的话,我试着给您举个栗子好了,假设有X和Y两个随机变量,X取值有X1,X2,Y 有Y1和Y2,我们就简单点,X有2种取值,Y也有2种取值,之后如果上升到N种取值时原理一样,我就不写那么复杂了,我大概证明下,同学看明白原理就行。
根据我们的描述,可以得到下图
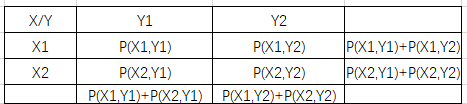
其中X1的概率是P(X1,Y1)+P(X1,Y2)
x2的概率是P(X2,Y1)+P(X2,Y2)
Y1和Y2我不写了,就是上图种最下面那行的2个
我们对X求期望,E(X)=X1*P(X1)+X2*P(X2)=X1*P(X1,Y1)+X1*P(X1,Y2)+X2*P(X2,Y1)+X2*P(X2,Y2)
同理可以写出E(Y)=Y1*P(X1,Y1)+Y1*P(X2,Y1)+Y2*P(X1,Y2)+Y2*P(X1,Y2)
接着我们写下E(X+Y)=(X1+Y1)*P(X1,Y1)+(X1+Y2)*P(X1,Y2)+(X1+Y2)*P(X1,Y2)+(X2+Y2)*P(X2,Y2)
把E(X+Y)展开后可以写出(X1+Y1)*P(X1,Y1)+(X1+Y2)*P(X1,Y2)+(X1+Y2)*P(X1,Y2)+(X2+Y2)*P(X2,Y2)=X1*P(X1)+X2*P(X2)=X1*P(X1,Y1)+X1*P(X1,Y2)+X2*P(X2,Y1)+X2*P(X2,Y2)+Y1*P(X1,Y1)+Y1*P(X2,Y1)+Y2*P(X1,Y2)+Y2*P(X1,Y2)
这个就是E(X)+E(Y)
当然这个是每个随机变量只有2个数,推广到多个数也一样。当然这个证明不要求掌握,只用第二条是个定理,直接用即可,就跟勾股定理一样,小学就会用,但是证明的话需要到高中学了余弦定理。FRM只要求会用这条定理即可,要证明是需要学了微积分和概率论之后
----------------------------------------------
虽然现在很辛苦,但努力过的感觉真的很好,加油!
pzqa27 · 2023年02月10日
嗨,从没放弃的小努力你好:
2.
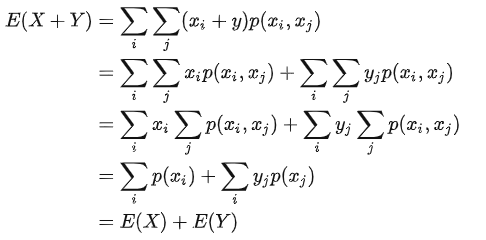
5.
令X为a1,a2,...an
aX=aa1,aa2,...aan
E(aX)=(a*a1+a*a2+..a*an)/n=a*[(a1+a2+a3+...an)/n]=a*E(x)
----------------------------------------------
虽然现在很辛苦,但努力过的感觉真的很好,加油!
梦梦 · 2023年02月11日
老师您好,实在不好意思,完全看不懂序号2解答的公式,能烦请您再详细解释一下每个等号的公式具体代表什么意思吗?比如第一个等号,不明白,X和Y代表两个随机变量,那x(i)、x(j)、y(j)分别是指什么意思?再比如第二个等号,第一个等号明明没有出现y(j),那为何出现y(j)?还有第三个等号到第四个等号是为什么也不明白呀。。。