NO.PZ202208160100000201
问题如下:
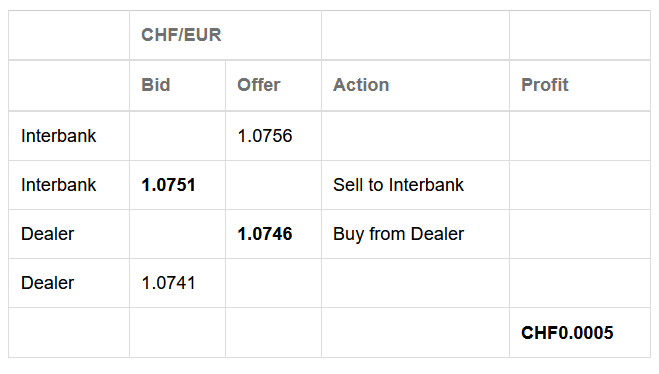
Based on the data in Exhibit 1, if a dealer quoted a bid–offer rate of CHF1.0741/EUR1.0746, then a profitable triangular arbitrage would most likely involve buying EUR1 from the dealer and then selling it in the interbank market for a profit of:选项:
A.CHF0.0005. B.CHF0.0008. C.CHF0.0007.解释:
Solution
A is correct. Calculate the CHF/EUR bid–offer cross rate implied by the interbank market using the equation CHF/EUR = (USD/CHF)–1 × USD/EUR = CHF/USD × USD/EUR. The equation shows that we have to invert the USD/CHF bid–offer quotes to get the CHF/USD bid–offer quotes.
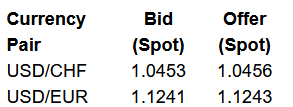
First, given the USD/CHF quotes of 1.0453/1.0456, take the inverse of each and interchange the bid and offer, such that the CHF/USD quotes are (1/1.0456)/(11.0453) = 0.95639/0.95666 = 0.9564/0.9567.
Then multiply the CHF/USD and USD/EUR bid–offer quotes:
Bid: 0.9564 × 1.1241 = 1.07509 = 1.0751
Offer: 0.9567 × 1.1243 = 1.07562 = 1.0756
Thus, the CHF/EUR cross-rate implied by the interbank market is 1.0751/1.0756.
The dealer is posting an offer rate to sell the EUR at a rate below the interbank bid rate. Thus, triangular arbitrage would involve buying EUR from the dealer at 1.0746 (offer) and selling it in the interbank market at 1.0751 (bid) for a profit of CHF0.0005 (1.0751 – 1.0746) per EUR.
B is incorrect. It erroneously inverts the USD/CHF quotes but does not interchange the bid and offer and thus incorrectly calculates the interbank market cross rate.
Bid: 0.9567 × 1.1241 = 1.07543 = 1.0754
Offer: 0.9564 × 1.1243 = 1.07528 = 1.0753
Thus, the CHF/EUR cross-rate implied by the interbank market is 1.0754/1.0753. (Note that the bid is higher than the offer.)
Triangular arbitrage would involve buying EUR from the dealer at 1.0746 (offer) and selling it in the interbank market at 1.0754 (bid) for a profit of CHF0.0008 (1.0754 – 1.0746) per EUR.
C is incorrect. It erroneously inverts the USD/CHF quotes but incorrectly calculates the interbank market cross-rate by mixing up the cross bids and offers.
Bid: 0.9564 × 1.1243 = 1.07528 = 1.0753
Offer: 0.9567 × 1.1241 = 1.07543 = 1.0754
Thus, the CHF/EUR cross-rate implied by the interbank market is 1.0753/1.0754.
Triangular arbitrage would involve buying EUR from the dealer at 1.0746 (offer) and selling it in the interbank market at 1.0753 (bid) for a profit of CHF0.0007 (1.0753 – 1.0746) per EUR.
不好意思,没看懂答案,能否画图并且解释一下