steepen时bullet是好的。但是为什么sell convexity不行？

ZCB的convexity不等于0哈。简单的理解，ZCB的duration会在债券的生命周期中发生变化，那么既然duration会发生变化，那么convexity就不会是0.

但是可以说，在相同duration的情况下，ZCB的Convexity最小，因为只有一笔现金流，而相同Duration的Coupon-paying bond 现金流更加分散。

以下是一个简单的数学推导，可以参考下，只做了解：

ZCB的债券价格：

把上述公式记为公式1

Duration:

Convexity:

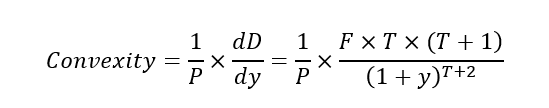
将公式1代入化简：

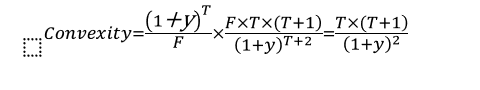
所以可以看出想让ZCB的convexity等于0，除非是T=0，即债券到期。

发现ZCB的Convexity与他的Maturity的平方成正比，所以有了讲义里的第二条结论：

再补充一下，duration是债券价格对利率的一阶导，Convexity是二阶导，从上面的债券价格变动的公式也能看出来duration对债券的影响占更大的比重。这也就是为什么只有较为精确考察时，才考虑convexity。

如果一个barbell债券组合，和另一个bullet债券组合，他们的duration相同，那么barbell债券组合的convexity是会更大的。

在这种情况下，如果利率曲线整体平行移动，例如利率下跌，如果仅仅用duration衡量，他俩的涨幅是一样的，但是如果在考虑Convevity的影响，barbell涨的更多，因为conveixty更大。同样，利率整体上升，barbell还是更好，由于convexity大，所以跌的少。

对于本题，在利率曲线非平行移动的情况下，首先要看的是债券组合的Key rate duration（最主要的影响）。barbell组合的KRD就决定了他在steepening（长期涨，短期跌）的变动情况下表现的更不好。最主要的影响已经决定了barbell不好，剩下次要的convexity影响太小。

你的理解有一点点偏差。

Conveixty对于债券来说，是一个好的“属性”。当利率发生小幅度变动时，我们可以只考虑duration，当利率发生大幅度变动时，需要既考虑duration，又考虑convexity，这样就会更精确的考察利率变动债券价格的变动。

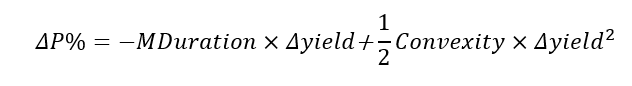
如上图，当利率发生变动时，债券价格百分比的变动：即考虑了前半部分的duration影响，又考虑了后半部分convexity影响。

发现当利率下跌时，公式右边前半部分duration带来的影响是使得债券价格上升，后半部分convexity的影响是进一步加强债券价格的上升幅度，因为后半部分是正数。

当利率上升时，公式右边前半部分duration带来的影响是使得债券价格下跌，但是后半部分convexity的影响是正数，所以可以一定程度上减轻债券价格下降的幅度。

利率曲线再更加steepening的情况下，假设长期利率上升，短期下跌；在这种情况下，为什么bullet会优于barbell，主要是因为债券组合的债券分布不同。

对于bullet的组合，更多的债券到期日集中在中期。这就是为什么他叫bullet，因为更多的现金流发生在中期。既然大多数的债券Maturity在中期，那么说明Macaulay duration，进一步说明Modified duration在中期。所以对于bullet组合，他的MD是中期的数据。

对于两个duration相同的债券组合，一个是barbell，一个是bullet。既然债券的加权平均duration一样，说明barbell的组合，主要的债券更多的集中在：长期，和短期。因为barbell是现金流更多的集中在两头，所以更多的债券到期日在两头，这样的加权平均MD才能和bullet一样。

所以一个steepening的曲线（长期利率上升，短期利率下跌），barbell型的组合表现更差，这是因为barbell组合的有很多duration大的债券，所以跌的更多。也有很多duration小的债券，但是duration很小，所以带来的上涨收益有限。

在这种steepening情况下，bullet表现的就更好，因为bullet更多的债券是中期duration的债券，长端和短段利率的变动对他的影响比较小。

其实Barbell和bullet，也可以看成key rate duration分布不同的债券。对于barbell，主要是长期和短期的key rate duration较大，中期的KRD较小。对于Bullet，主要是中期的KRD较大，短期、长期的KRD较小。因此Steepening（长期利率涨和短期利率跌的变动）对barbell的影响更大。

重新补图

这些策略的划分，首先先要确定利率曲线是否稳定，稳定的情况下对应4种情况；不稳定的情况下，还要判断利率曲线是怎么变得，是平行移动，还是变换曲度，不同的变动方式对应不同形状的portfolio。

这道题把我们在三级里学到的 active yield curve strategy 基本都列出来了。

根据预测未来的收益率曲线是否稳定做了以下分类：

债券的Convexity属性，对债券投资人来说是有利的属性。

因为当利率下跌时，相同duration情况下，凸性大的债券，其价格涨得更高。

当利率上升时，相同duration情况下，凸性大的债券，其价格跌得更少。

如果当投资者卖出Convexity时，意味着投资者认为未来利率的波动率较小，即投资者认为未来利率不会怎么变动，他是stable的。在利率不变stable、或者波动率小的情况下Convexity对投资者来说是没有价值的，因此，他可以出售掉convexity（卖出option）获取premiums，这个premiums可以增强投资者持有债券期间的收益。

本题A manager预测的是债券曲线会更加陡峭，即利率曲线有波动，在这种情况下Convexity是有价值的，卖出Convexity投资者要承担更大的风险。比如卖出call option来sell convexity，如果利率下降债券价格上升，投资者并不能享受债券价格上升带来的收益，因为bond很有可能被call option的对手方行权以低价买走。