对因为Risk neutral (PD) > actual PD, 因此PV(EL) >EL 如何推导出来的不理解。

同学你好。我先复述一下何老师的讲解，然后给你提供另外一个思路。

我们的PV(EL)采用的是迂回的办法求出来的，即求一个同条件的risk-free bond的现值，再求一个risky bond的现值，现值差价就代表了：PV(EL)

用公式表达就是：

其中等式右边的现值，可以用两种办法求：

对于Risky bond求现值，一种方法是对债券的现金流直接用 (risk-free rate + credit spread)折现。风险体现在折现率上。

第二种方法：就是在风险中性的假设下用risk-free rate折，风险体现在现金流的调整上。

不管用哪种方法，求出来的PV(Risky)是一样的，于是有以下公式（方便起见假设bond是一年到期的零息债券）：

等式左边风险体现在折现率上，等式右边分子是调整风险后的现金流。所以等式右边PD是风险中性下的违约概率。

上面公式经过一系列变形，得到了以下结论：

等式左边是对承担风险的额外补偿，等式右边是单位损失。

这个等式就意味着风险补偿完全补偿了expected loss (Credit risk).

原版书上在Reduced model基础上做了一定假设得到的同样的结论：

the credit spread is equal to the expected percentage loss per year on the risky zero-coupon bond.

the expected percentage loss per year implied by the credit spread.

继续看这个公式，

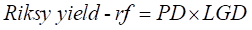
无论是用structural还是reduced-model，他都假设市场无摩擦，即没有liquidity premium，但我们知道，由于现实存在liquidity premium，所上面等式左边的补偿，还包括对流动性的补偿。但在计算右边的风险中性的PD时，把左边的补偿全部当做了对credit risk补偿，于是用上面的公式算出来的PD要大于实际的PD。

由于违约概率PD乘以LGD就是expected loss，在风险中性的情况下，PD更大所以算出来的Expected loss更大。所以风险中性下的expected loss大于实际的expected loss

如果风险中性情况下的expected loss足够大，以至于折现后的PV(expected loss)都比实际的expected loss大。那么在这种情况下，risk-neutral引起的credit spread提高起到主导因素。如果PV(EL)小于实际PD算出来的EL，那么说明Time-value起到主导因素，因为本身就高的风险中性expected loss折现后还小于实际expected loss。

第二种思路在用credit spread算PV(EL)时体现。

继续看这个公式，右边的PV(risky)还可以直接求：现金流用Risky-yield折现。如果credit spread达到一定程度，那么折现率就会足够大，那么使得PV(risky)足够小，减出来的PV(EL)就会很大。