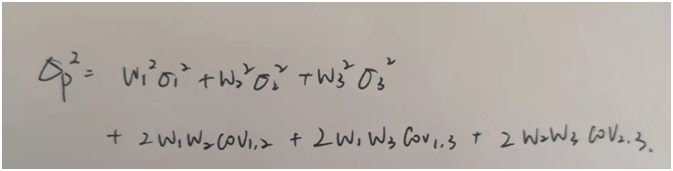NO.PZ2021062201000004
问题如下:
Lena Hunziger has designed the three-asset portfolio summarized below:
Hunziger estimated the portfolio return to be 6.3%. What is the portfolio standard deviation?
选项:
A.13.07%
B.13.88%
C.14.62%
解释:
C is correct. For a three-asset portfolio, the portfolio variance is:
=(0.20)2(196) + (0.30)2(225) + (0.50)2(400) + 2(0.20)(0.30)(105) + (2)(0.20)(0.50)(140) + (2)(0.30)(0.50)(150)
=7.84 + 20.25 + 100 + 12.6+ 28 +45
=213.69
知识点:Probability Concepts
看解答还是不是很清晰