NO.PZ2017092702000087
问题如下:
A portfolio has an expected mean return of 8 percent and standard deviation of 14 percent. The probability that its return falls between 8 and 11 percent is closest to:

选项:
A.8.3%
B.14.8%.
C.58.3%.
解释:
A is correct. P(8% ≤ Portfolio return ≤ 11%) = N(Z corresponding to 11%) - N(Z corresponding to 8%).
For the first term, Z = (11% – 8%)/14% = 0.21 approximately, and using the table of cumulative normal distribution given in the problem, N(0.21) = 0.5832.
To get the second term immediately, note that 8 percent is the mean, and for the normal distribution 50 percent of the probability lies on either side of the mean.
Therefore, N(Z corresponding to 8%) must equal 50 percent.
So P(8% ≤ Portfolio return ≤ 11%) = 0.5832 – 0.50 = 0.0832 or approximately 8.3 percent.
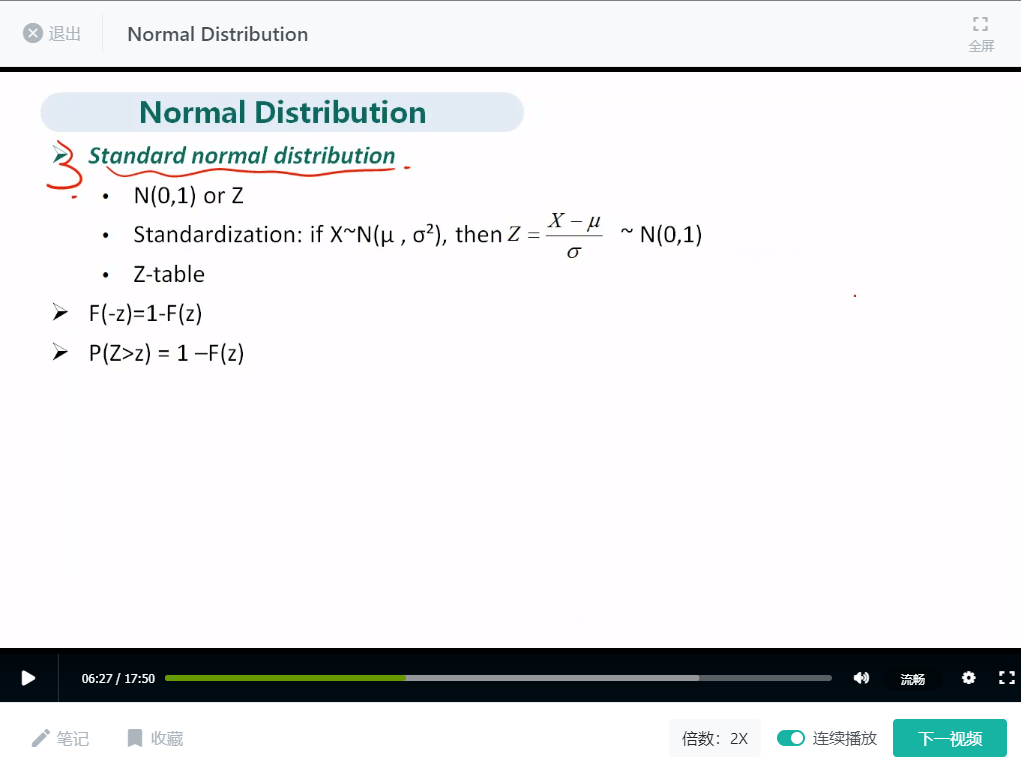
1.(11%-8%)/14%是对正态分布标准化的过程,直接套用标注化公式(X-均值)/标准差, 即可。
2. 标准化后得到的关键值就是Z值,之后可以通过查表求得对应的概率。比如N(0.5832)
3. 题目要求的P(8%<X<11%),我们可以求得P(X<11%)以及P(X<8%),再用前者减去后者
这是MODULE4 基础视频里第几个视频有知识点讲解?我重新看一遍,谢谢。