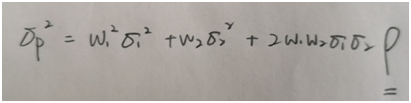NO.PZ2021062201000003
问题如下:
A two-stock portfolio includes stocks with the following characteristics:
What is the standard deviation of portfolio returns?
选项:
A.14.91%
B.18.56%
C.21.10%
解释:
B is correct. The covariance between the returns for the two stocks is
Cov (R1,R2) = ρ (R1,R2) σ (R1) σ(R2) = 0.20 (12) (25) = 60.
The portfolio variance is:
=(0.30)2(12)2+(0.7)2(25)2+2(0.30)(0.70)(60)
=12.96 +306.25 +25.2
=344.41
The portfolio standard deviation is:
知识点:Probability Concepts
这道题我一点都没看懂。。。 题干中不是已经给出了各个标准差的占比,问题就是两个组合之前的标准差是多少,为什么不能直接两个相加呢?