嗨,爱思考的PZer你好:
(1)这一点可以从theta的公式来理解,theta=期权价格的变化/时间的变化。当期权价格变化最大的时候,theta就大。而在ATM的时候,期权价格是变化最大的,因为当标的价格变化一点的时候,期权可能是OTM也可能是ITM的,可谓一念天堂一念地狱,所以期权价格变化最大,对应theta最大。
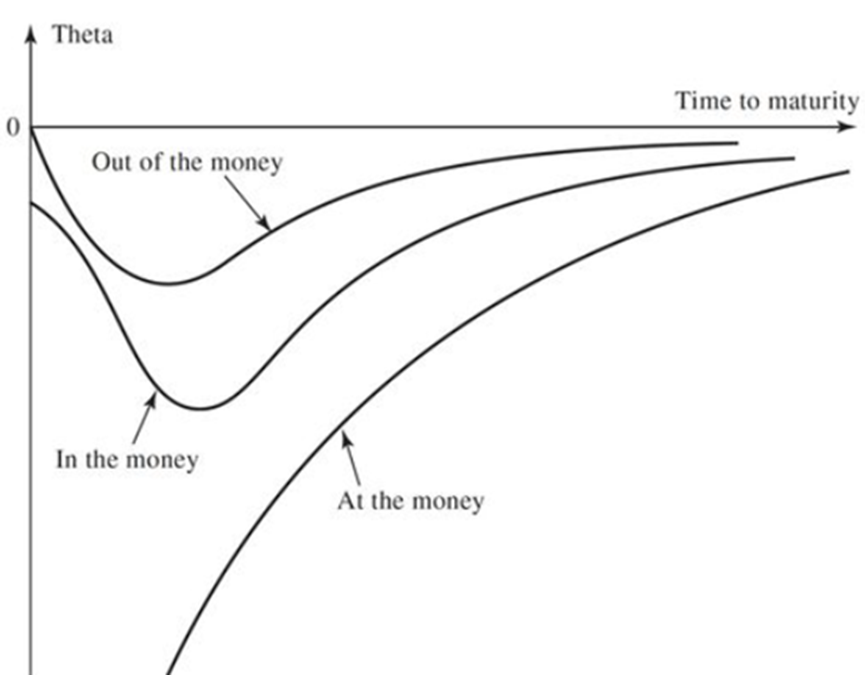
(2)另外可以参考John Hull期权期货和衍生品这本书上的一个图来看:(注意该图的横坐标是举例到期日的时间,因此最左边的0时刻表示到期日)此功能这个图也可以看到ATM的期权其theta是最大的。
gamma代表的是delta的变化速度。
ATM这个问题用极端情况来考虑会更容易理解,当call 越来越趋近于深度OTM(delta接近0)或深度ITM(delta接近1)时,斜率的变化会越来越小,相应的gamma也会越来越小,而只有在ATM的时候call处于两种状态的切换时点,斜率的变化是最大的。
gamma和时间有关系是因为delta和时间有关系,当越来越接近到期日的时候,期权到底属于价内还是价外状态就越来越确定,delta在ATM附近的数值变化幅度会越来越大,相应的gamma也会越来越大。
我这边放两张gamma的图来帮助你记忆,可以分别看出执行价对gamma,以及到期时间对gamma的影响。


----------------------------------------------
虽然现在很辛苦,但努力过的感觉真的很好,加油!







