Lumis Case Study
Lumis Ltd. is the registered investment adviser subsidiary of the Lumis family office. Thomas Lutz, who oversees fixed-income investment analysis for Lumis, seeks mispriced fixed-income securities in thinly traded markets. Lutz is discussing fixed-income valuation concepts with junior analyst Winston Fong and asks him to take notes.
Lutz explains: “The framework of the arbitrage-free value of a bond is central to identifying opportunities in inefficient markets for our portfolio. I am currently interested in developing market supranational debt, which is a part of the debt market that has not yet gained a large investor following. The International Economic Development Bank (IED Bank) has issued a four-year infrastructure financing bond at par with a 6.90% coupon; both are collectively backed by the member countries of the IED Bank.”
Fong states, “An arbitrage-free approach would discount each interest payment to the present using the corresponding rate on the yield curve. Therefore, in a positively sloped yield curve, the last interest coupon and principal payments at maturity would be discounted at a rate equal to the yield-to-maturity, while the discount rates applied to the annual interest payments prior to maturity would be lower than the discount rate applied to the cash flows occurring at maturity.”
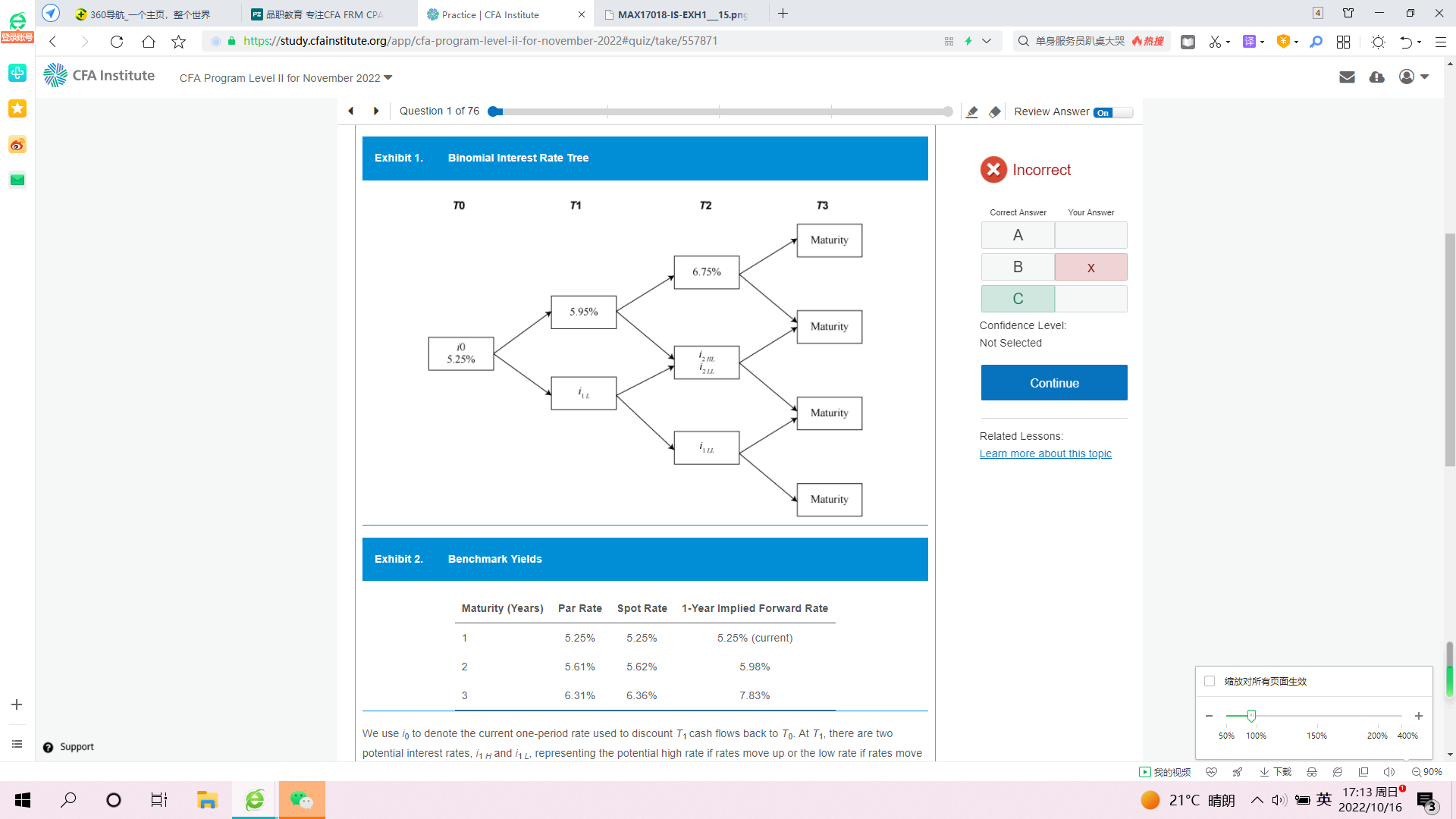
Lutz continues: “IED Bank has also issued a three-year callable bond at par. Callable bonds have cash flows that are not known in advance because they change depending on the level of interest rates. A visual representation of the values of future interest rates for use in valuing callable bonds can be presented with a binomial interest rate tree. The binomial tree in Exhibit 1 is incomplete; it is missing the interest rates at a few of its nodes. It is based on the yield curve shown in Exhibit 2.
Exhibit 1.
Binomial Interest Rate Tree
Exhibit 2.
Benchmark Yields
Maturity (Years)Par RateSpot Rate1-Year Implied Forward Rate15.25%5.25%5.25% (current)25.61%5.62%5.98%36.31%6.36%7.83%
We use i0 to denote the current one-period rate used to discount T1 cash flows back to T0. At T1, there are two potential interest rates, i1 H and i1 L, representing the potential high rate if rates move up or the low rate if rates move down. They are obtained by applying an interest rate model and an assumption of the volatility of interest rates. Using a lognormal random walk, we derive the three potential rates, i2 HH, i2 LL, and i2 HL, at T2. The i’s are known as nodes of the tree, and the period between interest payments are time steps. Our interest rate model is assuming i1 H will be 5.95%, i2 HH will be 6.75%, and the volatility of rates will exhibit a standard deviation of 15% within a lognormal tree structure.”
Fong begins to calculate the missing rates in the binomial tree and adds the following to his notes while doing so: “Using this yield curve information, i2 LL must be approximately 3.704%, must be close to 5.98% for a three-year bond, and the value at i3 LLH is 100.”
Lutz concludes: “After calculating the rates at each node, we must calibrate the rates within the interest rate tree to fit the current yield curve. This is an iterative process, where we select trial rates based on our model and raise or lower them until the rates match the term structure of the benchmark yield curve. Please try this for the binomial tree using the benchmark yields in Exhibit 2, starting with the trial rate for i1 H remaining at 5.95% and the standard deviation at 15%.”
Question
Fong’s notes regarding the construction of the binomial interest rate tree are least likely correct with respect to:
- the value at i2LL.
- the value at i2LH.
the value at i3LLH.