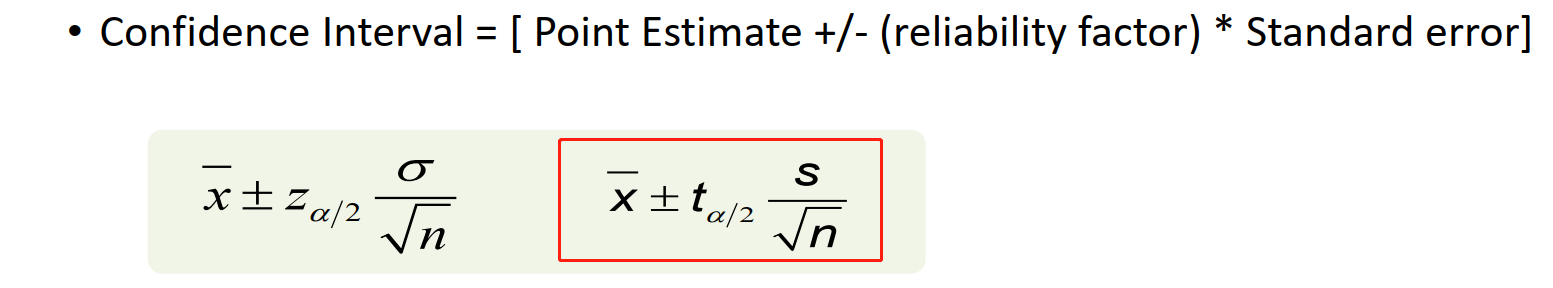NO.PZ2022071202000071
问题如下：
QuestionUse the following values from a student’s t-distribution to establish a 95% confidence interval for the population mean given a sample size of 10, a sample mean of 6.25, and a sample standard deviation of 12. Assume that the population from which the sample is drawn is normally distributed and that the population variance is not known.
The 95% confidence interval is closest to a:
选项：
A.lower bound of -2.20 and an upper bound of 14.70. B.lower bound of -0.71 and an upper bound of 13.21. C.lower bound of -2.33 and an upper bound of 14.83.解释：
Solution
C is correct. With a sample size of 10, there are 9 degrees of freedom. The confidence interval concept is based on a two-tailed approach. For a 95% confidence interval, 2.5% of the distribution will be in each tail. Thus, the correct t-statistic to use is 2.262.
The confidence interval is calculated as:ˉX±t0.025 s/√nwhere ˉX is the sample mean, s is the sample standard deviation, and n is the sample size. In this case: 6.25 ± 2.262 × 12/√10 = 6.25 ± 8.58369 or -2.33 to 14.83.
A is incorrect: it uses the t-statistic for 10 degrees of freedom, not 9: 6.25 ± 2.228 × 12/√10.
B is incorrect: it uses the t-statistic for p = 0.05 rather than p =0.025: 6.25 ± 1.833 × 12/√10.
解析没看懂，可以请老师细讲一下吗？
