NO.PZ2017092702000012
问题如下:
A sweepstakes winner may select either a perpetuity of £2,000 a month beginning with the first payment in one month or an immediate lump sum payment of £350,000. If the annual discount rate is 6% compounded monthly, the present value of the perpetuity is:
选项:
A.less than the lump sum.
B.equal to the lump sum.
C.greater than the lump sum.
解释:
C is correct.
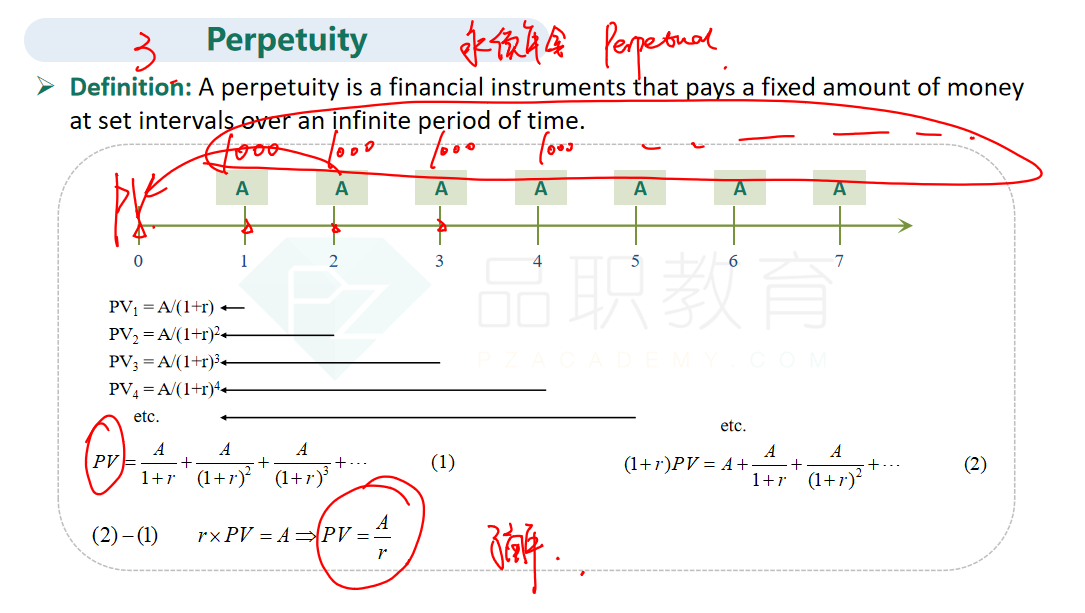
As shown below, the present value (PV) of a £2,000 per month perpetuity is worth approximately £400,000 at a 6% annual rate compounded monthly. Thus, the present value of the annuity (A) is worth more than the lump sum offer. A = £2,000 r = (6%/12) = 0.005 PV = (A/r) PV = (£2,000/0.005) PV = £400,000
the present value of the“perpetuity”--永续年金,带入永续年金的公式 PV=A/r即可:
A=2,000, r=(6%/12)=0.005, PV=A/r=400,000
为什么不用(1+6%/12)^1的EAR公式计算有效年利率呢,不是每月复利一次吗,然后再用这个利率算年金的PV