计算债券YTM的時候,是假設票息以YTM再投资,这个在现实世界中怎么理解?
假设设100元买入票息位5.25%的债券,3年后100元赎回,YTM是5.25%;但如果沒進行再投資,實現的年化收益也還是5.25%呀?
求解答
发亮_品职助教 · 2022年05月25日
嗨,爱思考的PZer你好:
计算债券YTM的時候,是假設票息以YTM再投资,这个在现实世界中怎么理解?假设设100元买入票息位5.25%的债券,3年后100元赎回,YTM是5.25%;但如果沒進行再投資,實現的年化收益也還是5.25%呀?
提问说的这种情况,是期间的Coupon再投资的利率为0,所以最终投资债券获得的收益率是小于5.25%的。
只有当期间Coupon的再投资利率是5.25%时,才能保证债券的实际投资收益也是5.25%
Coupon是需要进行再投资的,这是从债券的折现公式角度理解的:就是债券的折现公式就假设了债券的投资期间,期间的所有现金流(Coupon)都是以期初买入债券时的YTM进行再投资的。只有达到这个要求,才能使得期初的投资实现YTM的收益。
注意,这个条件很难满足。因为在现实世界中,我们投资债券之后,往往市场中的利率是动态变化的,于是债券投资期间获得的现金流(Coupon)实际上很难以期初恒定的YTM进行再投资,所以在期初买入债券时确定的这个YTM,只能是对投资债券实现收益的一个预估,我们实际投资债券获得的收益一般情况下是不等于期初的YTM的,只有当期间的再投资利率没有发生改变,一直是YTM时,投资债券获得的收益才是YTM。
下面用公式展示一下这个说法,假设是一个2年期的债券,我们期初以85元买入,那么债券的折现公式是这样:
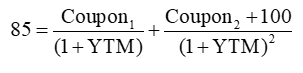
注意,上面式子中,Coupon1与Coupon2数值上是一样大的,只是为了区分时间的差异,所以把第一年收到的Coupon标记为Coupon1,把第2年收到的Coupon标记为Coupon2.
我们给这个等式做一个变形,就是等号的左右两边同时乘以(1+YTM)^2,则变成:
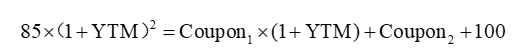
这个等号的左边,85×(1+YTM)^2,代表的意思是:期初我们用85元买入债券,然后投资这两年实现了YTM的收益;
那85元投资要实现这个YTM的收益,我们需要满足什么条件呢?
实际等号的右边就告诉了我们需要实现的条件,即,第一年拿到的Coupon1必须要以YTM进行再投资1年,这是式子Coupon 1×(1+YTM)告诉我们的,同时第2年年末还能够顺利足额的拿到债券的现金流(Coupon2+100)
所以,投资债券想要实现YTM的收益,就必须要保证期间的现金流Coupon1能以YTM进行再投资。
如果期间的Coupon1再投资的利率比YTM要低,那么显然等号不可能成立,于是投资债券85元实际获得的收益肯定小于期初的YTM
如果期间的Coupon1再投资的利率比YTM要高,那么等号也不会成立,但因为期间的再投资收益更高,所以导致债券的实际投资收益高于期初的YTM。
----------------------------------------------努力的时光都是限量版,加油!